Aufgabe:
Wir verallgemeinern das Problem aus Aufgabe 1(c) jetzt durch das Hinzufügen eine Nichtlinearität in jeder Komponente \( (2 \leq i \leq n-1) \) :
\( f_{i}(u):=(A u)_{i}+\lambda u_{i}\left(u_{i}-1\right), \)
sowie \( f_{1}(u)=(A u)_{1} \) und \( f_{n}(u)=(A u)_{n} \). Nun betrachten wir das nichtlineare Problem \( f(u)=b \). Wir wollen dies per Fixpunktiteration lösen. Als Abbruchkriterium wählen Sie bitte für das Residuum \( \|f(u)\|_{2} \leq \) tol mit tol \( =10^{-8} \).
(a) Formulieren Sie \( f(u)=b \) als Fixpunktproblem und implementieren Sie diese Funktion und eine Fixpunktiteration.
(b) Lösen Sie damit das obige Problem für \( n=5 \) und \( \lambda=10^{-3} \) mit dem Anfangswert: \( u=(0, \ldots, 0) \). Dokumentieren Sie die Ergebnisse durch die Ausgabe von Iterationsschritt, Residuum in jeder Iteration und visualisieren Sie wieder die Lösung vergleichend mit der aus Aufgabe 1 (zu \( n=5) \).
Problem/Ansatz:
Hey, ich habe folgende Funktion: f(u) + u - b = u
f(u) ist dabei folgendermaßen Aufgebaut: 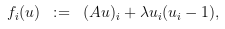
u ist folgender Vektor: (4.4408920985006264E-17, 0.06694176000000003, 0.08925568000000002, 0.06694176, 0.0)
b ist folgender Vektor: (1.115696, 1.115696, 1.115696, 0.26776704, 0.0)
Als Beschreibung wie eine Fixpunktiteration funktioniert habe ich folgendes bekommen:
\( f_{i}(u):=(A u)_{i}+\lambda u_{i}\left(u_{i}-1\right) \)
1. Wähle Startwert \( x^{(0)} \in M \), und setze \( k=0 \).
2. Setze \( x^{(k+1)}:=f\left(x^{(k)}\right) \).
3. Ist
\( d_{X}\left(f\left(x^{(k+1)}\right)-x^{(k+1)}\right)<\epsilon \)
dann STOP, sonst \( k \rightarrow k+1 \) und fahre fort mit 2 .
Leider stehe ich nun sehr auf dem Schlauch... wie genau muss ich hier vorgehen?