Zwei Graphen schneiden sich nicht

Question

Aufgabe:

Gegeben sind die beiden in ℝ definierten Funktionen f und g mit f(x)= e^x+1/2x+1 und g(x)=1/2x
Die Graphen der beiden Funktionen sind in Abbildung 1 dargestellt.

(1) Begründen Sie, dass der Graph von f und der Graph von g keinen gemeinsamen Punkt besitzen.

(2) Bestimmen Sie den Inhalt der Fläche, die von den Graphen von f und g , der y-Achse und der parallel zur y-Achse verlaufenden Geraden mit der Gleichung x = 1 eingeschlossen wird

Problem/Ansatz:

Aufgabe kriege ich nicht gelöst

Comments

Ausführlichere / Verbesserte Version:

Titel: BestimmenSiedenInhaltderFläche,dievonden Graphen von f und g , der y-Achse und der parallel zur y-Achse verlaufenden …

Stichworte: parallel,integral

Aufgabe: F(x)= e^x+1/2x+1 und g(x)=1/2x

BestimmenSiedenInhaltderFläche,dievonden Graphen von f und g , der y-Achse und der parallel zur y-Achse verlaufenden Geraden
mit der Gleichung x = 1 eingeschlossen wird.

Problem/Ansatz: Man muss ja jetzt eine Integralrechnung machen, aber bei mir kommt die ganze Zeit was anderes raus als in den Lösungen steht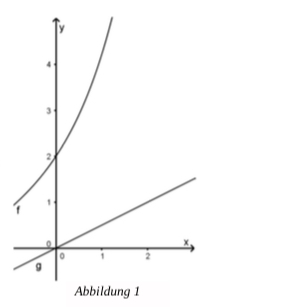

Text erkannt:

Abbildung 1

Answer 1

Bilde die Differenz f(x)-g(x).

Was erhältst du?

Begründe dann, dass diese Differenz immer positiv ist.

Comments

Bei mir kommt e^x= -1 raus

In den Lösungen steht auch das die Gleichung keine Lösung hat, also reicht das als Begründung?

---

Bei mir kommt e^x= -1 raus

Da soll doch keine Gleichung rauskommen. Du solltest lediglich einen Differenzterm bilden, und der ist e^x+1.

Man sollte wissen, dass e^x immer positiv ist (und e^x + 1 noch ein wenig positiver). Also ist f(x) immer größer als g(x).

---

Okey das macht Sinn, nur in den Lösungen steht halt e^x=-1 , weshalb ich etwas verwirrt bin

Answer 2

(2) Bestimmen Sie den Inhalt der Fläche...

Hier integrierst Du die von Abakus erwähnte Differenzfunktion von 0 bis 1.

Comments

Es geht um diese Fläche:

Answer 3

f(x)= e^x + 1/2x + 1
g(x)=1/2x
d ( x ) = f ( x ) - g ( x )
d ( x ) = e^x + 1/2x + 1 - ( 1/2 * x )
d ( x ) = e^x + 1
Stammfunktion
S = e^x + x
S zwischen 0 und 1
e^1 + 1 - ( e^0 + 0 )

e + 1 - 1
A = e