es geht um die Zerlegung der Helmholtz Gleichung in Kugelkoordinaten, also Seperationsansatz.
Separiere ich erhalte ich folgende drei Gleichungen:
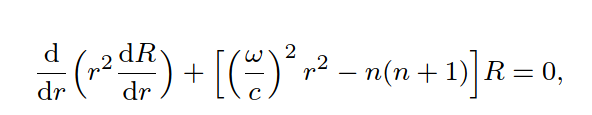
Text erkannt:
\( \frac{\mathrm{d}}{\mathrm{d} r}\left(r^{2} \frac{\mathrm{d} R}{\mathrm{~d} r}\right)+\left[\left(\frac{\omega}{c}\right)^{2} r^{2}-n(n+1)\right] R=0 \)
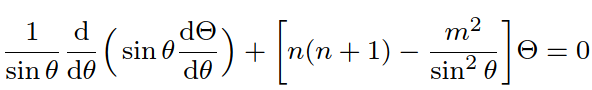
Text erkannt:
\( \frac{1}{\sin \theta} \frac{\mathrm{d}}{\mathrm{d} \theta}\left(\sin \theta \frac{\mathrm{d} \Theta}{\mathrm{d} \theta}\right)+\left[n(n+1)-\frac{m^{2}}{\sin ^{2} \theta}\right] \Theta=0 \)
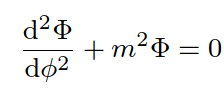
Text erkannt:
\( \frac{\mathrm{d}^{2} \Phi}{\mathrm{d} \phi^{2}}+m^{2} \Phi=0 \)
Die Konstanten m und (n+1)*n so einzuführen haben wir als Tipp in der Übung bekommen. Ich denke das hat was mit der Legendre DGL zu tun und bei m vielleicht mit der Beschränktheit der Lösung? Nun sollen wir die ersten zwei DGLs in die Bessel DGL und in die Legendre DGL überführen durch Substitutionen. Ich hab jetzt schon eine Weile probiert, aber ohne Hilfe komme ich nicht weiter und wahrscheinlich nie zum Ziel. Bin in Substitution, aber auch immer eine kleine Niete gewesen. Kann mir wer helfen, besonders die 2te bräuchte ich.