Raute in einem Rechteck berechnen

Question

Aufgabe:

Gegeben ist ein rechteck in welchem eine Raute herausgeschnitten wird (siehe Bild)

Gegeben sind a 6dm und b 3dm

Problem/Ansatz:

Wie berechne ich nun x und den flächeninhalt beider dreicke welche endstehen?

Answer 1

Hallo,

In einer Raute stehen die Diagonalen senkrecht auf einander

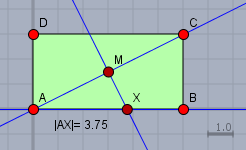
somit sind die Dreieck \(\triangle ABC\) und \(AMX\) änlich und es gilt (\(x=|AX|\) und die Diagonale \(|AC|\) sei \(d\))$$\frac{x}{d/2} = \frac{d}{a}$$Auflösen nach \(x\) und Einsetzen der gegebenen Werte gibt:$$\begin{aligned} \frac{x}{d/2} &= \frac{d}{a} \\ \implies x &= \frac{d^2}{2a} \\ x &= \frac{a^2+b^2}{2a}\\ &= \frac{6^2+3^2}{2 \cdot 6} = \frac{15}{4}= 3,75 \end{aligned}$$Die Fläche \(F\) der Raute ist dann wie beim Parallelogramm schlicht Grundseite mal Höhe, also \(F=x\cdot b\).

Gruß Werner

Answer 2

Wie berechne ich nun x

x = √((6 - x)^2 + 3^2) --> x = 3.75 dm

und den flächeninhalt beider dreicke welche endstehen

A = (6 - 3.75)·3 = 6.75 dm²