Berechnung der Fläche mit Integral

Question

Aufgabe:

Berechnung mit Hilfe eines Integrales

Problem/Ansatz:

Könnte man dieses Problem mit Hilfe eines Integrales berechnen wenn ja könnte es mir jemand erklären danke.

Comments

Deine Frage hat mich bewogen, auch hier

https://www.mathelounge.de/923717/flacheninhalt-eines-kleeblatts

noch eine Antwort nachzureichen.

Auch bei der Frage besteht die Diskrepanz zwischen "prinzipiell möglich" und "praktisch suboptimal".

---

Grundsätzlich kann man ∫ (a bis b) (f(x) - g(x)) dx rechnen, wobei f(x) die obere und g(x) die untere Berandung ist.

Meist wird es natürlich vereinfacht gemacht das f(x) und oder g(x) in mehrere Teilfunktionen für verschiedene Intervalle aufgesplittet wird. Aber theoretisch langt ein Integral dafür.

---

Aber theoretisch langt ein Integral dafür.

Dann zeige mal praktisch, wie es "theoretisch" in einem Zug geht.

---

g(x) = 3(125-8x)*sgn(x-17)/40-3(8x+125)*sgn(x+17)/40+(29x^2+1152x-18000)*sgn(x-12)/1920-(29x^2-1152x-18000)*sgn(x+12)/1920

Aber das nur, weil Wolframalpha keine Stückweise definierten Funktionen hat.

Die CAS Systeme von Texas Instruments und Casio können abschnittsweise definierte Funktionen verarbeiten und auch integrieren.

---

Aber das nur, weil Wolframalpha keine Stückweise definierten Funktionen hat.

Doch, hat es.

---

Doch, hat es.

Dann würde ich mich freuen, wenn du erklärst, wie man das dort eingibt.

Mit Wolframalpha kenne ich mich wirklich nicht gut aus.

Hat sich erledigt.

https://www.wolframalpha.com/input/?i=piecewise+function

---

Ohne das Ergebnis wirklich zu prüfen könnte das vermutlich in Wolframalpha so aussehen

Zumindest wenn der Bogen über eine Parabel modelliert werden kann. Aber auch mit anderen modellierungen sollte das so über ein Integral gehen.

Answer 1

Könnte man dieses Problem mit Hilfe eines Integrales berechnen

Nein.

Comments

Wieso nicht?

---

siehe Antwort von Abakus

Für den Bogen sind zwar die Koordinaten von drei Punkten bekannt (grün eingezeichnet), aber nicht ob er ein Kreis oder eine Parabel oder sonst etwas sein soll.

Wäre das bekannt, dann wäre der Kreis oder die Parabel definiert und man könnte die Fläche integrieren.

Answer 2

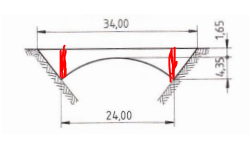
Ja, das geht mit Integralrechnung., Du kannst es nur nicht in einem Ritt berechnen, weil du drei (oder zumindest zwei) unterschiedliche Situationen hast. Die linke und die rechte Teilfläche sind Flächen zwischen den Funktionsgraphen einer oberen konstanten Funktion und einer unteren linearen Funktion.

Die mittlere Teilfläche wird oben von einer konstanten Funktion und unten von der Funktion begrenzt, die den Bogen beschreibt.

Da du uns jede Information verweigerst, ob es sich dabei um einen Kreisbogen, um eine Parabel oder einen anderen Funktionstyp handelt, kann die Hilfe nicht konkreter sein.

Im Falle eines Kreisbogens wäre Integralrechnung so ziemlich die schlechteste Wahl.

Comments

Im Falle eines Kreisbogens berechnet sich die mit 34,00 angegebene Streckenlänge unter Verwendung der anderen drei Maße zu 34,0

Nachtrag : In meiner Berechnung steckt außerdem noch ein rechter Winkel drin, da würde ich dann eher vermuten, dass dieser eben kein rechter ist als dass der Bogen kein Kreisbogen ist.

---

Nachtrag (nachdem zwei Parabelansätze vorgeschlagen wurden) :
Zwischen einem Parabel- und einem Kreisbogen ist mit bloßem Auge tatsächlich nicht zu unterscheiden, wie diese

Ausschnittsvergrößerung zeigt.

Answer 3

Könnte man dieses Problem mit Hilfe eines
Integrales berechnen

Da steht ja nicht

Könnte man dieses Problem mit Hilfe nur eines
Integrales berechnen

Sprachlich sind also mehrere Deutungen möglich

Ebenso
Nutze zur Berechnung die Integralrechnung

Parabelbogen
( 0 | -1.35 )
( 12 | -6 )
( -12 | -6 )

f(x) = -31/960·x^2 - 27/20

usw.

Was meint der Fragesteller dazu ?