Betrachte mal den Ball mit Mittelpunkt O:=(0,0)
Wenn du jetzt einen Punkt P:=(x,y) ungleich (0,0) betrachest, bilden die beiden Punkte eine Ursprungsgerade, der Abstand zwischen den Punkten berechnet sich also immer nach dem ersten Fall:
$$ d(O,P) = || (x,y) - (0,0) || = \sqrt{x^2 + y^2} < r = 1 $$
der Ball einfach nur eine offene Kreisscheibe mit Radius 1.
Jetzt O:=(1,0)
Für alle Punkte P:=(x,0) auf der x-Achse leigen die Punkte auf einer Ursprungsgeraden und wir haben den Fall 1.
$$ d(O,P) = || (x,0) - (1,0) || = |x-1| < r = 1 $$
Also liegen alle Punkte P mit |x-1| < 1 im Ball drin
Für übrige Punkte Q:=(x,y) mit y≠0 liegen O und Q nicht mehr auf einer Ursprungsgerade hier ist dann der zweite Fall anzuwenden
$$ d(O,Q) = || (x,y) || +|| (1,0) || = \sqrt{x^2+y^2} + |1| < r = 1 $$
Somit liegen nur Punkte Q im Ball für die \( 0 < |y| \le \sqrt{x^2+y^2} < 0 \) gilt. Das ist nie erfüllt. Der offene Ball besteht hier deshalb nur aus den Punkten P.
Wenn du das ganze mal mit r = 1.5 betrachtest sieht das so aus:
Punkte P=(x,0) liegen drin falls |x-1| < 1.5
Punkte Q=(x,y) legen drin falls \( \sqrt{x^2+y^2} < 0.5 \)
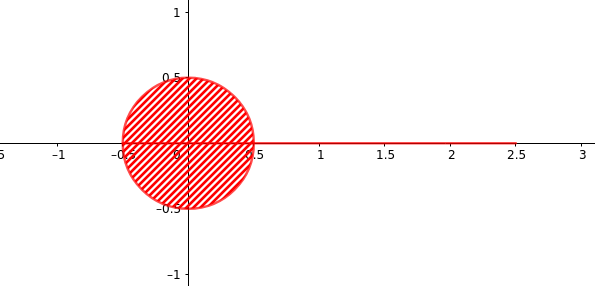
Das ist also so ein offener Ball mit Stiel dran.