Potenzreihe Konvergenzbereich bestimmen Grenzwert Folge

Question

Aufgabe: Grenzwert der Folge bestimmen

…

Problem/Ansatz:Wie kommt man hier auf  d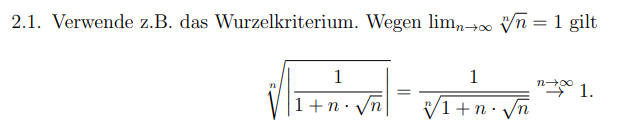

Text erkannt:

2.1. Verwende z.B. das Wurzelkriterium. Wegen \( \lim \limits_{n \rightarrow \infty} \sqrt[n]{n}=1 \) gilt
\( \sqrt[n]{\left|\frac{1}{1+n \cdot \sqrt{n}}\right|}=\frac{1}{\sqrt[n]{1+n \cdot \sqrt{n}}} \stackrel{n \rightarrow \infty}{\rightarrow} 1 . \)

en den Grenzwert 1.Ein zusätzlicher Zwischenschritt wäre nützlich.

Answer 1

Man hat$$a_n:=\sqrt[n]{2n^2}\geq \sqrt[n]{1+n\sqrt{n}}\geq \sqrt[n]{n}=:b_n$$Nun ist \(\lim a_n=\lim\sqrt[n]{2}\cdot \lim \sqrt[n]{n}\cdot \lim\sqrt[n]{n}=1\cdot 1\cdot 1=1\)

und \(\lim b_n=1\). Nach dem Sandwich-Lemma (Quetsch-Lemma)  folgt die

Behauptung.