Aufgabe:
Ein Spiel- und Sportgerätehersteller produziert Drachen vom Typ „Trendy“.
Der Drachen besteht aus einem Segel, welches durch ein Gestänge aufgespannt wird. Für das Gestänge werden die Stäbe AC und BD im Punkt M miteinander verbunden, das ebene Segel ABCD besitzt die Form eines Rhomus.
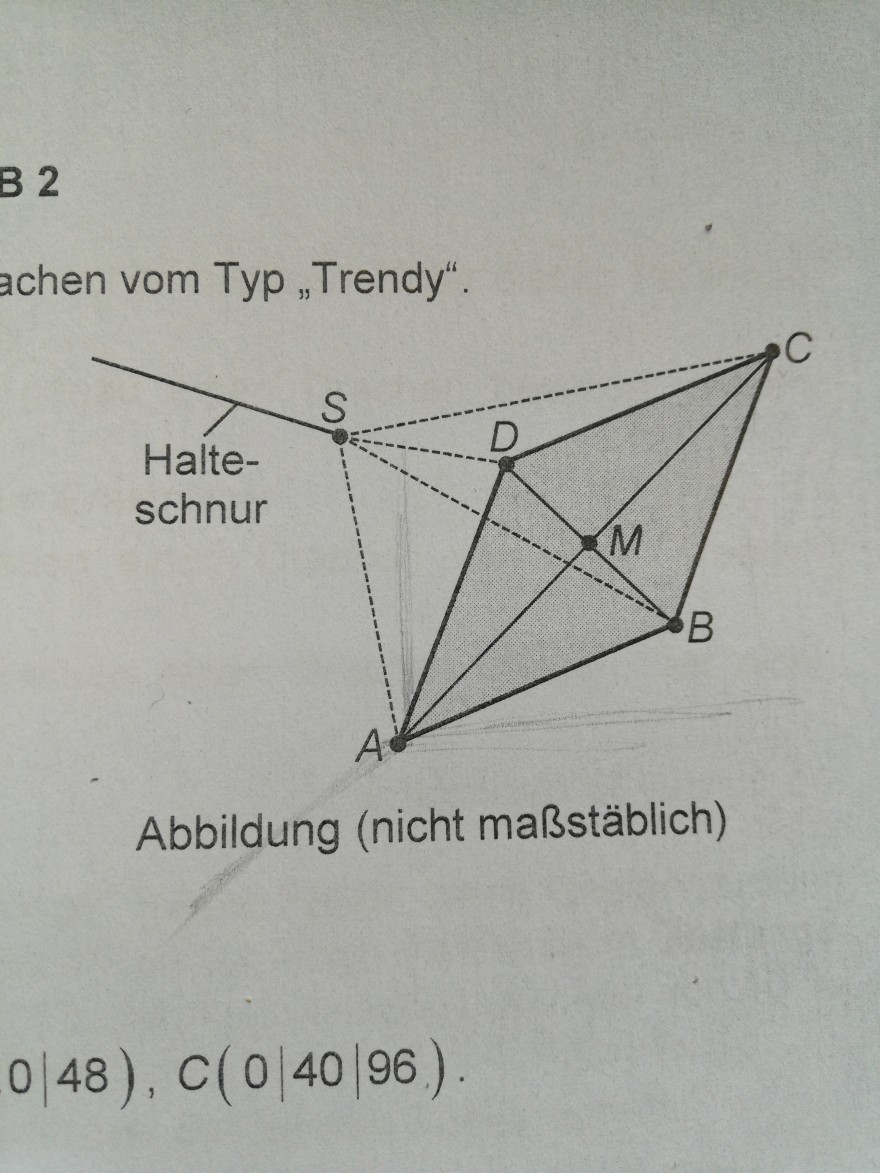
An dem Drachen werden in den Punkten A, B, C und D Nylonseile befestigt, welche in einem gemeinsamen Punkt S zusammenlaufen (siehe Abbildung).
Für die Punktkoordinaten gilt: ( A(0|0| 0), B(30|20| 48), C(0|40| 96), D(-30|20| 48), S(0l56l33)
Der Drachen liegt stabil im Wind, wenn die straff gespannten Nylonseile AS & CS sowie BS & DS jeweils gleich lang sind.
der Punkt C des Segels wird so verändert, dass ein Drachenviereck ABC'D mit dem Flächeninhalt 2340cm² entsteht. Gesucht ist die Koordinate von C'
Der Spiel- und Sportgerätehersteller verändert den Punkt C des Segels von „Trendy " so, dass ein Drachenviereck ABC'D mit dem Flächeninhalt 2340cm² entsteht.
Ermitteln Sie die Koordinaten des Punktes C'.
Problem/Ansatz:
Ich bin davon ausgegangen dass der Punkt C trotzdem noch in der yz Ebene liegt und somit x=0 gilt?
trotzdem bräuchte ich doch eine weitere koordinate um den punkt c' mit der formel des flächeninhalts über solve zu ermitteln? Ich hab schon überlegt zwecks orthogonalität von e & f im drachenviereck ...
hat wer weitere Lösungsansätze
?
Text erkannt:
32
achen vom Typ "Trendy".
Abbildung (nicht maßstäblich)
\( 0 \mid 48), C(0|40| 96) . \)