Gibt es dazu eine allgemeine Formel?
Na ja! - ich meine die Frage nach der Formel ist immer die falsche Frage. Aber wenn Du schon fragst ....
Die Parabel hat eine bestimmte Eigenschaft:
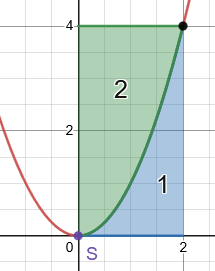
Verläuft die Parabel durch die beiden gegenüberliegenden Eckpunkte eines achsenparallelen Rechtecks und befindet sich ihr Scheitelpunkt in einem der beiden Ecken, so teilt die Parabel die Fläche des Rechteck immer im Verhältnis \(2\div 1\).
Daraus folgt dann auch unmittelbar, dass diese grüne Fläche ....
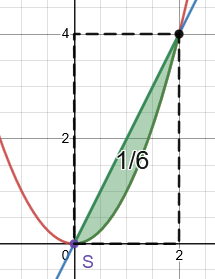
... die durch die Diagonale und die Parabel begrenzt ist, immer ein Sechstel der Fläche des Rechtecks ist.
Übertragen auf Deine Aufgabe heißt das: Die Fläche \(F_{hf}\) zwischen \(h(x)\) und \(f(x)\) ist$$F_{hf} = \frac 16 \cdot 2 \cdot 4 = \frac43$$und die Fläche \(F_{gf}\)zwischen \(g(x)\) und \(f(x)\) $$F_{gf} = \frac16 \cdot \frac43 \cdot\underbrace{\left(4-g\left(\frac43\right)\right)}_{=\frac{16}9}=\frac{32}{81}$$und dann ist$$F = F_{hf} - F_{gf} = \frac43 - \frac{32}{81}=\frac{76}{81}$$
und hab jetzt als Ergebnis 76/81 raus. Passt das?
... und Dein Ergebnis passt. Und noch das BIld zum Text
https://www.desmos.com/calculator/8xgxlqi2bf
Gruß Werner
