Dann vergleiche mal die vorgegebenen Lösungen

mit dem, was du uns geliefert hast:
x=((√(n^(2)-4*√(2))+n)/(2)).
Finde den Fehler.
PS:
Ich habe in der Frage beim Ergebnis lediglich x und n vertauscht gehabt.
Das hast du uns aber in deiner originalen Fragestellung nicht mitgeteilt!
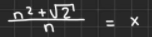
Multipliziere mit n!
Subtrahiere nx!
Löse die quadratische Gleichung!