Bestimmen Sie optimale Konstanten m und M

Question

Aufgabe:

Für \( d \in \mathbb{N} \) und \( v \in \mathbb{R}^{d} \) seien

\( \|v\|_{1}:=\sum \limits_{i=1}^{d}\left|v_{i}\right|,\|v\|_{2}:=\sqrt{\sum \limits_{i=1}^{\alpha}\left|v_{i}\right|^{2}} \text { und }\|v\|_{\infty}:=\max _{i=1_{1}, \ldots, d}\left|v_{i}\right| \)

Bestimmen Sie optimale Konstanten \( m_{i} \) und \( M_{i}, i \in\{1,2,3\} \), Sodass
a) \( m_{1}\|v\|_{\infty} \leq\|v\|_{1} \leq M_{1}\|v\|_{\infty} \).
b) \( m_{2}\|v\|_{\infty} \leqslant\|v\|_{2} \leqslant M_{2}\left\|_{v}\right\|_{\infty} \).
c) \( m_{3}\|v\|_{2} \leqslant\|v\|_{1} \leqslant M_{3}\|v\|_{2} \)

Problem/Ansatz:

Hallo
Ich verstehe folgende Aufgabe nicht.

Danke im Voraus

Gruß

Answer 1

Ich nehme mal als Beispiel \(m_1,M_1\):

Sei \(v\neq 0\), dann können wir die Ungleichungen (a) durch

\(\|v\|_1\) teilen:

\(m_1\cdot \|w\|_{\infty}\leq 1\leq M_1\cdot \|w\|_{\infty}\) mit \(\|w\|_1=1\).

Wir suchen also

\(m_1=\frac{1}{\max \|w\|_{\infty}}\) und

\(M_1=\frac{1}{\min \|w\|_{\infty}}\),

wobei \(w\) die "<Norm1-Einheitssphäre" \(\{w: \; \|w\|_1=1\}\) durchläuft.

Hieraus habe ich \(m_1=1\) und \(M_1=n\) erhalten.

Answer 2

Hallo,

Ich verstehe folgende Aufgabe nicht.

Bei dem Ausdruck \(\|v\|_p\) handelt es sich um eine sogenannte p-Norm. Bekannt ist Dir sicher die Euklidische Norm \(\|v\|_2\), die nichts anders ist, als der Betrag (anschaulich die Länge) des Vektors \(v\).

Allgemein gilt, wenn \(d\) die Dimension (die Anzahl der Koordinaten) von \(v\) ist:$$\|v\|_p = \left(\sum\limits_{k=1}^d |v_k|^p \right)^\frac 1d$$Also bei einem 2-dimensionalen Vektor wäre das mit \(p=2\) der bekannte Betrag$$\left\|v\right\| _2= \left\|\begin{pmatrix}x\\y\end{pmatrix}\right\|_2 = \left(x^2+y^2\right)^\frac12 = \sqrt{x^2+y^2}$$Vergleiche z.B. die Normen mit \(p=1\) (der Summennorm) mit der Euklidischen Norm \(p=2\) von einem Vektor in der Ebene

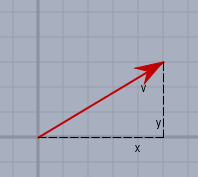
Die Summennorm \((p=1)\) von \(v\) ist hier$$\|v\|_1 = \left(\sum\limits_{k=1}^2 |v_k|\right)^{\frac11} = |x| + |y|$$und dieser Wert ist immer größer bzw. bestenfalls gleich groß wie die Länge von \(v\). Das besagt auch die Dreiecksungleichung$$|v| \le |x|+|y| $$D,h. in der Schreibweise der Norm$$\|v\|_2 \le \|v\|_1$$bzw. es gilt genauso allgemein$$\|v\|_p \le \|v\|_q \quad 0 \lt q \le p$$Umso größer das \(p\) desto kleiner die Norm.

Betrachten wir dann den ersten Teil der Aufgabe c)$$m_3 \|v\|_2 \le \|v\|_1$$Wenn man \(m_3=0\) setzt, so ist das natürlich immer erfüllt. Jetzt ist aber nach der 'optimalen Konstante' gefragt. Ich interpretiere das so, dass der Wert von \(m_3\) gesucht ist, für den die Ungleichung gerade noch gilt.

Und da sowieso immer \(\|v\|_2 \le \|v\|_1\) erfüllt ist (s.o.), ist hier schlicht \(m_3=1\). Was ist aber mit \(M_3\)?$$\|v\|_1 \le M_3\|v\|_2$$\(M_3\) mus sicher \(M_3\ge 1\) sein, um diese Ungleichung zu erfüllen. Aber wie groß mindestens, damit es für jedes \(v\) gilt?

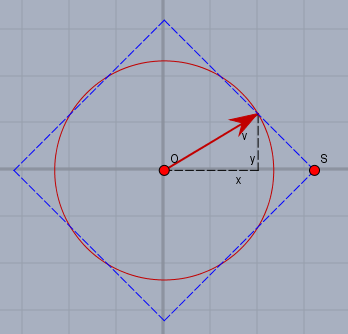
Nemen wir an, die Länge von \(v\) also \(\|v\|_2\) wäre fest. Oben im Bild ist $$\|v\|_1= |x|+|y|=|OS|$$ also die Länge der Strecke \(OS\). Wenn man den Vektor \(v\) auf der roten Kreisbahn bewegt, würde das Quadrat stets seine Größe verändern. Mit welchem Faktor \(M_3\) muss man die Länge multiplizieren, damit das Produkt mindestens so groß ist wie \(\|v\|_1\) also die Summe der Beträge der beiden Koordinaten? Oder anders gefragt: welche Position muss \(v\) auf dem Kreis einnehmen, damit das Quadrat möglichst groß ist, bzw. die Länge \(|OS|\) maximal wird?

Offensichtlich dann, wenn \(|x|=|y|\) gilt, also der Kreis vollständig in dem Quadrat aufgenommen wird. Und dann ist $$|x|=|y| \implies \|v\|_1 = |OS|=  \sqrt 2 \cdot \|v\|_2$$im 3-dimensionale wird der Kreis zu einer Kugel und das Quadrat zu einem Oktaeder. Hier wäre dann der Faktor \(M_3\) von der halben Diagonale zum Radius der Kugel \(M_3=\sqrt 3\). Und für den allgemeinen Fall betrachte man einen Vektor \(v\) mit gleich großen Koordinaten \(a\)$$v \in \mathbb R^d \quad v_k= a \space\forall k \in [1\dots d]\\\|v\|_1 = \sum\limits_{k=1}^d a = ad\\ \|v\|_2 = \sqrt{\sum\limits_{k=1}^d a^2}= a\sqrt d\\\implies M_3 = \frac{ad}{a\sqrt d}= \sqrt d$$Und mit dem Wissen mache Dich bitte mal an die Aufgaben a) und b). Falls Du noch Fragen hast, so melde Dich bitte.

Gruß Werner