Zeigen Sie folgende Abschätzung:

Question

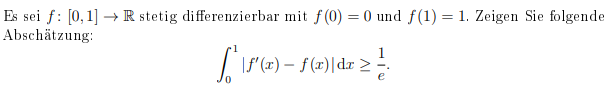
Text erkannt:

Es sei \( f:[0,1] \rightarrow \mathbb{R} \) stetig differenzierbar mit \( f(0)=0 \) und \( f(1)=1 \). Zeigen Sie folgende Abschätzung:
\( \int \limits_{0}^{1}\left|f^{\prime}(x)-f(x)\right| \mathrm{d} x \geq \frac{1}{e} . \)

Bin am Verzweifeln ich kriege diese Aufgabe einfach nicht gebacken. Gibt es hier jemanden der das hier vielleicht anschaulich lösen kann?

Answer 1

Sei $$ h(x) = e^{-x} f(x) $$ dann gilt $$ \frac{1}{e} = h(1)-h(0) = \int_0^1 h'(x) dx \le \int_0^1 |h'(x)| dx $$

Also

$$ \int_0^1 | e^x h'(x) | dx \ge \int_0^1 | h'(x) | dx \ge \frac{1}{e} $$