Hallo,
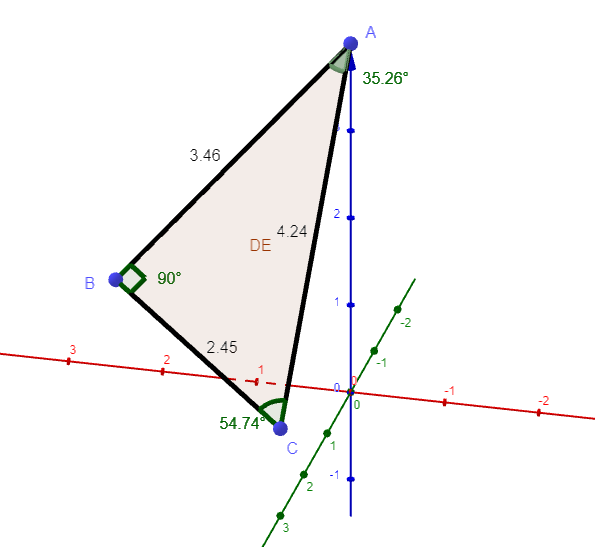
Zeigen Sie. dass das Dreieck rechtwinklig ist.
Wenn das Skalarprodukt zweier Vektoren null ergibt, dann bilden diese Vektoren einen rechten Winkel.
Den Winkel zwischen zwei Vektoren kannst du berechnen mit
\( \cos \alpha=\frac{\vec{a} \cdot \vec{b}}{|\vec{a} \cdot| \vec{b} \mid} \) mit \( 0 \leq \alpha \leq 180^{\circ} \)
und deren Länge mit
\( \vec{v}=\left(\begin{array}{l}x \\ y \\ z\end{array}\right) \quad|\vec{v}|=\sqrt{x^{2}+y^{2}+z^{2}} \)
zur Kontrolle hier die Zeichnung:
Gruß, Silvia