Hallo Laura,
Ich weiß nicht wie ich das einzeichnen soll.
rechne zunächst mal die gegebenen Maße mit dem Massstab um. Es ist$$5,00\,\text m \to 500\,\text{cm}\div 40 = 12,5\,\text{cm}\\3,00\,\text m \to 300\,\text{cm}\div 40 = 7,5\,\text{cm}\\1,20\,\text m \to 120\,\text{cm}\div 40 = 3,0\,\text{cm}$$Dann zeichne eine waagerechte Gerade (hier rot) und trage die Abmessungen wie unten gezeigt ein:
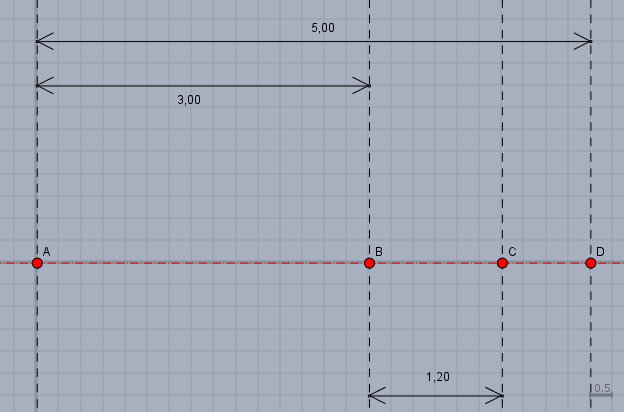
auf dem normalen Kästchenpapier geht das ganz prima!
Anschließend halbiere die Strecke \(BC\). Der Mittelpunkt ist \(M_{BC}\). Und dann halbiere die Strecke \(|AM_{BC}|\). Deren Mittelpunkt sei \(M'\). Und nun zeichne mit dem Zirkel einen Kreis um den Mittelpunkt \(M_{BC}\) mit Radius \(|M_{BC}C|\) und einen zweiten Kreis um \(M'\) mit dem Radius \(|M'A|\).
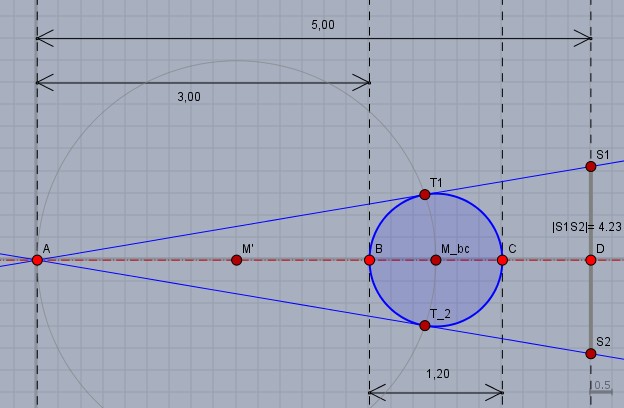
Die beiden Kreise schneiden sich in zwei Punkten \(T_1\) und \(T_2\). Und dann kannst Du die beiden Tangenten durch \(A\) und \(T_1\) und \(A\) und \(T_2\) einzeichnen.
Die Tangenten schneiden die "Wand" rechts in \(S_1\) und \(S_2\). Der Abstand zwischen diesen beiden Punkten ist dann die Breite des Schattens.
Gruß Werner