Grenzwertbestimmung nicht möglich

Question

Aufgabe:

Guten Tag, hallo,

ich komme bei einer Grenzwertbestimmung nicht weiter. Ich habe auch schon anderwertig gesucht, aber ich komme bei folgender Aufgabe leider zu keinen Ergebnis. Auch der TR, spuckt kein Ergebnis aus, ob ein Grenzwert existiert oder nicht.

Hier ist die Aufgabe

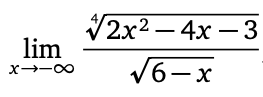
Text erkannt:

\( \lim \limits_{x \rightarrow-\infty} \frac{\sqrt[4]{2 x^{2}-4 x-3}}{\sqrt{6-x}} \)

Ich bedanke mich jetzt schon für eure Hilfe!

Problem/Ansatz:

Siehe oben

Answer 1

Verwende: a^(1/4)/ b^(1/2) = ((a^(1/2))^/(1/2))/ b^(1/2)=  ((a^(1/2)/b))^(1/2)

Kürze in der Klammer mit x!

Comments

Ja genau, aber wie wende ich diese Rechenregel nun genau an?

Answer 2

Ich setze \(y:=-x\). Dann geht es um den Limes von$$\frac{(2y^2+4y-3)^{1/4}}{(y+6)^{1/2}}\text{ für } y\rightarrow \infty\\\frac{(2y^2+4y-3)^{1/4}}{(y^2+12y+36)^{1/4}}=\left(\frac {y^2(2+4/y-3/y^2)}{y^2(1+12/y+36/y^2)}\right)^{1/4}=\left(\frac {2+4/y-3/y^2}{1+12/y+36/y^2}\right)^{1/4}\\\rightarrow \left(\frac{2+0-0}{1+0+0}\right)^{1/4}=\sqrt[4]{2}$$

Answer 3

Aloha :)

Willkommen in der Mathelounge... \o/

Da \(x\to-\infty\) gehen soll, sei im Folgenden \(x<0\) vorausgesetzt:$$\frac{\sqrt[4]{2x^2-4x-3}}{\sqrt{6-x}}=\frac{\sqrt[4]{x^2\left(2-\frac4x-\frac{3}{x^2}\right)}}{\sqrt{-x\left(-\frac6x+1\right)}}=\frac{\sqrt[4]{x^2}\cdot\sqrt[4]{2-\frac4x-\frac{3}{x^2}}}{\sqrt{-x}\cdot\sqrt{1-\frac6x}}=\frac{\sqrt[4]{2-\frac4x-\frac{3}{x^2}}}{\sqrt{1-\frac6x}}$$Wegen \(\sqrt{-x}=\sqrt[4]{(-x)^2}=\sqrt[4]{x^2}\) können wir kürzen:$$\phantom{\frac{\sqrt[4]{2x^2-4x-3}}{\sqrt{6-x}}}=\frac{\sqrt[4]{2-\frac4x-\frac{3}{x^2}}}{\sqrt{1-\frac6x}}\stackrel{(x\to-\infty)}{\to}\frac{\sqrt[4]{2+0-0}}{\sqrt{1+0}}=\sqrt[4]{2}$$