was ist hier die Norm von A und B?

Question

Text erkannt:

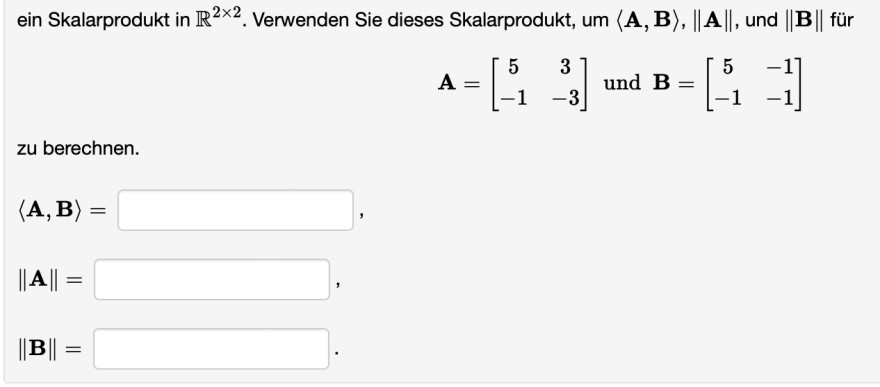
ein Skalarprodukt in $\mathbb{R}^{2 \times 2}$. Verwenden Sie dieses Skalarprodukt, um $\langle\mathbf{A}, \mathbf{B}\rangle,\|\mathbf{A}\|$, und $\|\mathbf{B}\|$ für
$\mathbf{A}=\left[\begin{array}{cc} 5 & 3 \\ -1 & -3 \end{array}\right] \text { und } \mathbf{B}=\left[\begin{array}{cc} 5 & -1 \\ -1 & -1 \end{array}\right]$
zu berechnen.
$\langle\mathbf{A}, \mathbf{B}\rangle=$
$\|\mathbf{A}\|=$
$\|\mathbf{B}\|=$

Problem/Ansatz:

was ist hier die Norm von A und B? ist das die größte Zahl im Matrix ?

Comments

Text erkannt:

$A=\left[\begin{array}{cc}5 & 3 \\ -1 & -3\end{array}\right]$
$B=\left[\begin{array}{cc}5 & -1 \\ -1 & -1\end{array}\right]$
$-A, B\rangle=5 \cdot 5+3 \cdot(-1)+(-1) \cdot(-1)+(-3) \cdot(-1)=26$
$\|A\|=$
$\|B\|=$

---

ein Skalarprodukt in $\mathbb{R}^{2 \times 2}$.

Du musst uns schon verraten, wie das Skalarprodukt

definiert ist !

---

Sisi, es gibt nicht das eine Skalarprodukt. Daher fehlt bei der Aufgabe der entscheidende Teil, in dem das zu verwendende Skalarprodukt definiert wird.

Ohne diese Angabe kann dir keiner wirklich helfen.

---

Text erkannt:

Seien
$\mathbf{A}=\left[\begin{array}{ll} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array}\right] \text { und } \mathbf{B}=\left[\begin{array}{ll} b_{11} & b_{12} \\ b_{21} & b_{22} \end{array}\right]$
Matrizen aus $\mathbb{R}^{2 \times 2}$. Dann definiert die Abbildung
$\langle\mathbf{A}, \mathbf{B}\rangle=a_{11} b_{11}+a_{12} b_{12}+a_{21} b_{21}+a_{22} b_{22}$

Answer 1

Aloha :)

Bei dem gegebenen Skalarprodukt werden die Matrix-Elemente an gleicher Position miteinander multipliziert und die Ergebnisse summiert:

$$\left<A|B\right>=25-3+1+3=26$$$$\|A\|^2=\left<A|A\right>=25+9+1+9=44\implies\|A\|=\sqrt{44}\approx6,6332$$$$\|B\|^2=\left<B|B\right>=25+1+1+1=28\implies\|B\|=\sqrt{28}\approx5,2915$$

Answer 2

Die Norm jeder Matrix ist hier dann wohl

die Wurzel aus dem Skalarprodukt der Matrix mit sich selbst.