Hey
Ich habe die folgende Aufgabe gerechnet.
ich möchte nur wissen, ob mein Lösung richtig ist.
Mein lösungsweg ist:
V= 1/6 * (Det |AB AC AD|)
AB= (-4|2|4) AC=(0|3|0) AD=(-2|-4|2)
Det |AB AC AD| = 0
deswegen das Volumen =0
danke für eure Hilfe :)
Text erkannt:
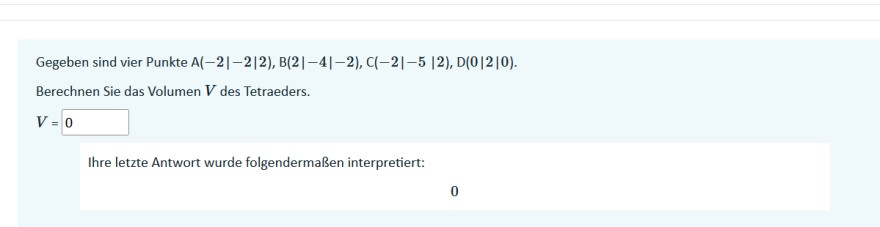
Gegeben sind vier Punkte \( A(-2|-2| 2), B(2|-4|-2), C(-2|-5| 2), D(0|2| 0) \).
Berechnen Sie das Volumen \( V \) des Tetraeders.
\( V=0 \)
Ihre letzte Antwort wurde folgendermaßen interpretiert:
0
Text erkannt:
MATHEMATIK 1B - MINITESTS - SS 22
Startseite / Meine Kurse / Mathe \( 1 \mathrm{~B} \) - Minitests - 5522 / Minitest 3 "Geraden und Ebenen" / Minitest zu Geraden und Ebenen