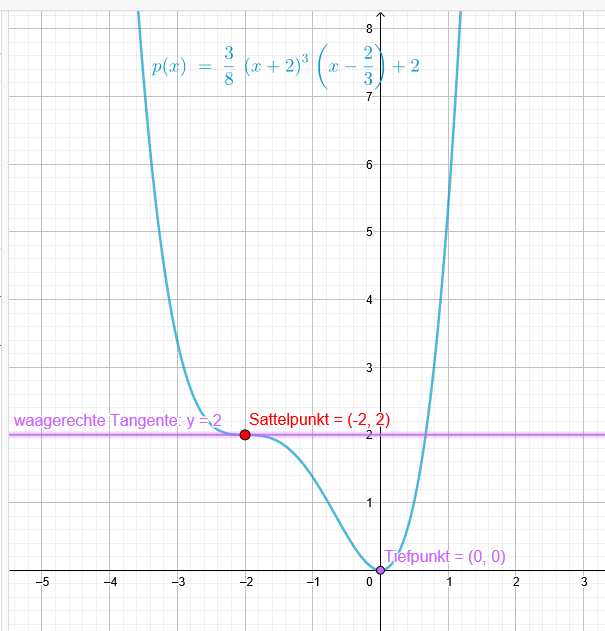
Ein Graph einer ganzrationalen Funktion hat den Sattelpunkt S(-2|2) und den Tiefpunkt T(0|0) . Bestimme die Gleichung mit möglichst niedrigen Grad.
Ich verschiebe um 2 Einheiten nach unten und mache weiter mit der Nullstellenform der Parabel 4.Grades:
Sattelpunkt S´(-2|0)→dreifache Nullstelle T(0|0) T´(0|-2)
\(f(x)=a*(x+2)^3*(x-N)\)
\(f(0)=a*(0+2)^3*(0-N)=-8a*N\)
\(-8a*N=-2\) → \(a=\frac{1}{4N}\)
\(f(x)=\frac{1}{4N}*[(x+2)^3*(x-N)]\)
\(f´(x)=\frac{1}{4N}*[3*(x+2)^2*(x-N)+(x+2)^3]\)
\(f´(0)=\frac{1}{4N}*[3*(0+2)^2*(0-N)+(0+2)^3]\)
\(f´(0)=\frac{1}{4N}*[-12N+8]\)
\(f´(0)=0\)
\(\frac{1}{4N}*[-12N+8]=0→N=\frac{2}{3}\) \(a=\frac{1}{4*\frac{2}{3}}=\frac{3}{8}\)
\(f(x)=\frac{3}{8}*(x+2)^3*(x-\frac{2}{3})\)
Nun 2 Einheiten nach oben:
\(p(x)=\frac{3}{8}*(x+2)^3*(x-\frac{2}{3})+2\)