Aufgabe:
Überlappende Fläche berechnen.
Problem/Ansatz:
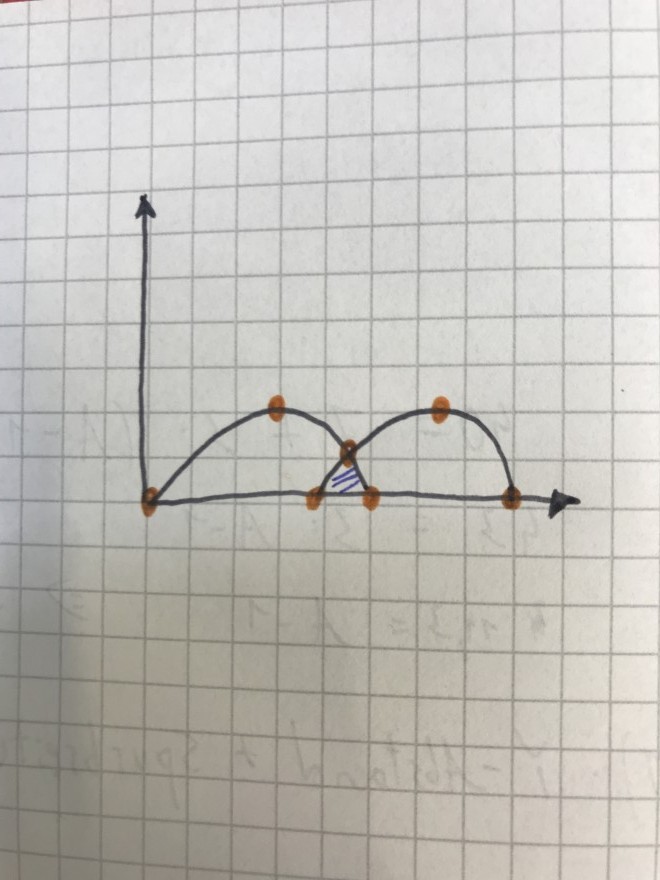
Hey, ich habe zwei Funktionen (beide bekannt) und 6 bekannte Punkte (Orange). Der siebte Punkt (die Schnittstelle) lässt sich ja berechnen. Ist also ebenfalls bekannt.
Nun möchte ich die überlappende Fläche der beiden Graphen (blau schraffiert) möglichst elegant lösen. Die beiden Graphen sind übrigens in ihrer Gestalt gleich, der eine ist nur um den Wert x auf der Achse verschoben.
Leider komme ich auf keinen Lösungsweg. Würde mich freuen, wenn mir jemand einen Tipp geben kann.
Nicht wundern, in der Skizze sind keine Werte, da ich das gerne selber Lösen möchte. Ich muss nur die Vorgehensweise wissen.
Danke für die Hilfe
VG