Aufgabe:
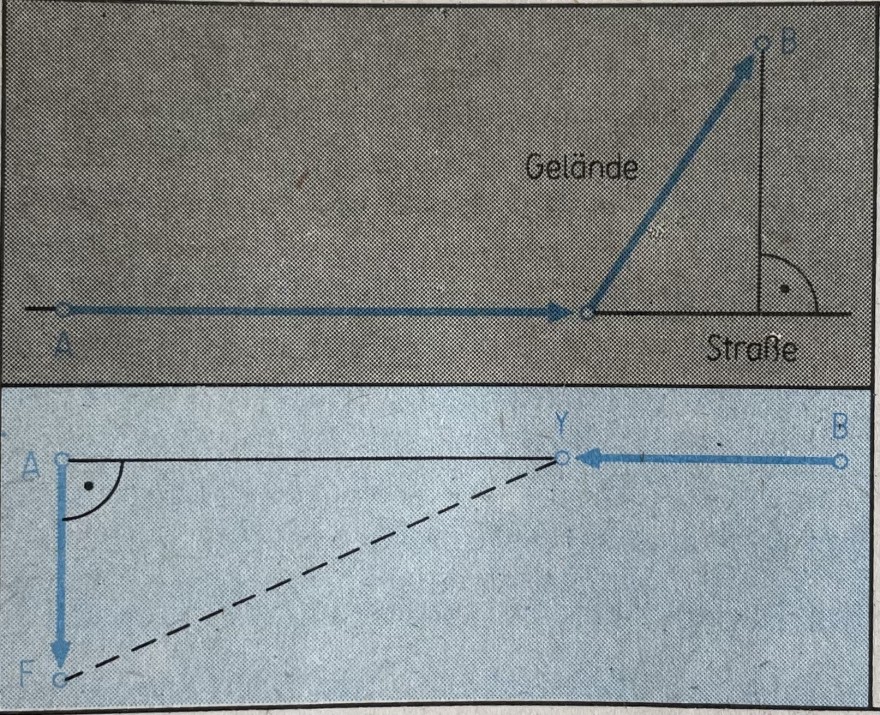
Fine Artillerie-Einheit der Nationalen Volksarmee hat einen Stellungswechsel von A nach
B durchzuführen. Während A an einer geradlinig verlaufenden Straße
liegt, ist Bein 12 km von der Straße entfernt liegender Geländepunkt. Der Fußpunkt des
Lotes von B auf die Straße ist 20 km von A entfernt. Die Marschgeschwindigkeit der
Einheit beträgt auf der Straße v1 = 50 kmh-1 und im Gelände v2 = 25 kmh-1. An
welcher Stelle muß die Kolonne von der Straße abbiegen, um den Stellungswechsel in
möglichst kurzer Zeit zu vollziehen?
Gelande
09
Problem/Ansatz: Ich habe keine Ahnung wie ich diese Aufgabe lösen soll, ein nachvollziehbarerer Lösungsweg wäre daher sehr hilfreich.