Aufgabe:
Entscheiden Sie, ob die durch f : ℝ → ℝ,
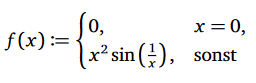
Text erkannt:
\( f(x):=\left\{\begin{array}{ll}0, & x=0 \\ x^{2} \sin \left(\frac{1}{x}\right), & \text { sonst }\end{array}\right. \)
definierte Funktion in x0 = 0 differenzierbar ist. Falls ja, bestimmen Sie f ′(0). Skizzieren
Sie den Graphen der Funktion.
Problem/Ansatz:
Guten Abend.
Grundsätzlich komme ich mit dieser Angabe mal gar nicht zurecht. Aber ich versuche euch mal zu verdeutlichen was ich darunter verstehe. Ich verstehe darunter, das wenn x gleich 0 ist, das f(x) dann einfach null ist, und für alle anderen Werte gilt f(x) = x²*sin(1/x). Aber wie gebe ich das ganze zum Beispiel in einen Rechner ein, das es bestimmt wird. F abgeleitet 0 ist dann ja null oder nicht? Hoffe es kann mir hier wer helfen.