\(f(x)=2 x^{3}-150 x+5 \)
\(f´(x)=6 x^{2}-150 \)
\(6 x^{2}-150 =0→x^2=25 \)
\(x₁=5→f(5)=250-750+5=-495\)
Art des Extremwerts:
\(f´´(x)=12 x \) \(f´´(5)=60>0 → Minimum \)
\(x₂=-5→f(-5)=2* (-5)^{3}-150 *(-5)+5=505\)
Art des Extremwerts:
\(f´´(x)=12 x \) \(f´´(-5)=-60<0 →Maximum \)
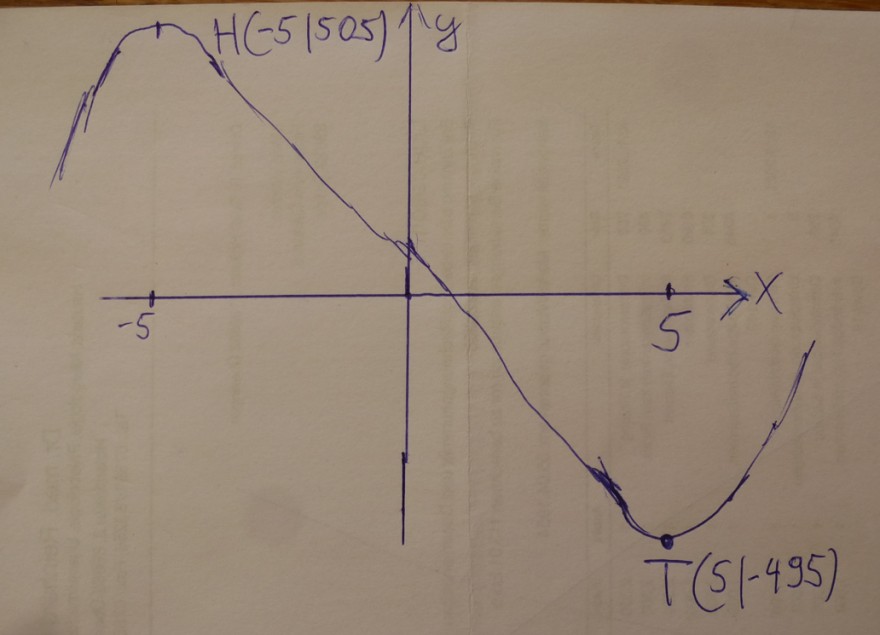
Das Minimum liegt bei T(5|-495), und das Maximum liegt bei H(-5|505)
Im Intervall \({-5<x<5}\) ist \(f(x)\) streng monoton fallend.