Aufgabe:
A.
Würfeln Sie 36 mal mit einem Würfel und erstellen Sie ein Diagramm wie häufig jede Augenzahl vorkommt. Zeichen Sie in das Diagramm noch die erwartete Häufigkeit für jede Augenzahl ein.
B.
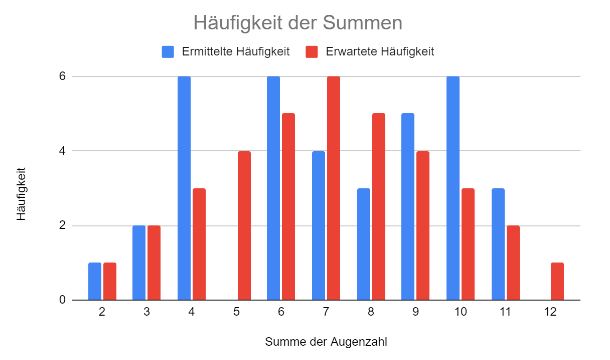
Würfeln Sie 36 mal mit zwei Würfeln und erstellen Sie ein Diagramm wie häufig jede Summe der Augenzahlen vorkommt. Zeichen Sie in das Diagramm noch die erwartete Häufigkeit für jede Summe ein.
C.
Es ist aus der Statistik bekannt, dass der Fehler einer Stichprobe (und das ist eine endliche
Anzahl Würfeln nun mal) von der Größe der Stichprobe abhängt.
Wenn n die Größe der Stichprobe ist, dann ist +/- √ der Standardfehler:
Ermittelt man den Wert n einer Stichprobe, dann liegt der ‚wahre‘ Wert zwischen
+ √ und - √, oder kurz geschrieben in +/- √ mit einer Wahrscheinlichkeit von
ca. 67%.
a. Zeichnen Sie dieses Vertrauensintervall in die Diagramme A und B ein und beurteilen Sie jetzt die Ergebnisse.
Problem/Ansatz:
ich habe ein Verständnisproblem bei der Aufgabe C. Die Aufgabe A und B habe schon gemacht und nochmal in diesem Text aufgeschrieben, damit der Zusammenhang zur Aufgabe C klar wird.
In der Aufgabe A und B wurde 36 mal gewürfelt. Die Zahl 36 entspricht also unserer Stichprobengröße n, womit der Standardfehler +/- 6 beträgt.
Der “wahre” Wert liegt somit zwischen 30-42 mit einer Wahrscheinlichkeit von ca. 67%.
Nun ist mir leider nicht klar, wie ich ein Vertrauensintervall in meine Diagramme einzeichnen kann.
Diagramm A: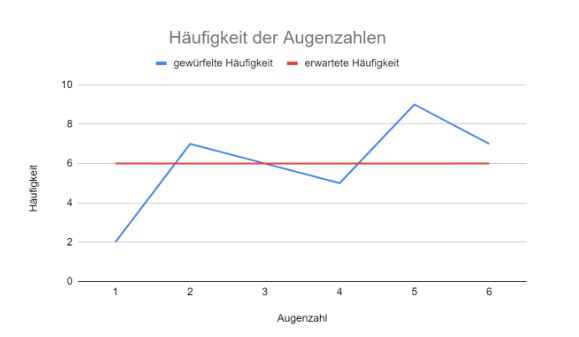
Diagramm B: