Aufgabe:
Text erkannt:
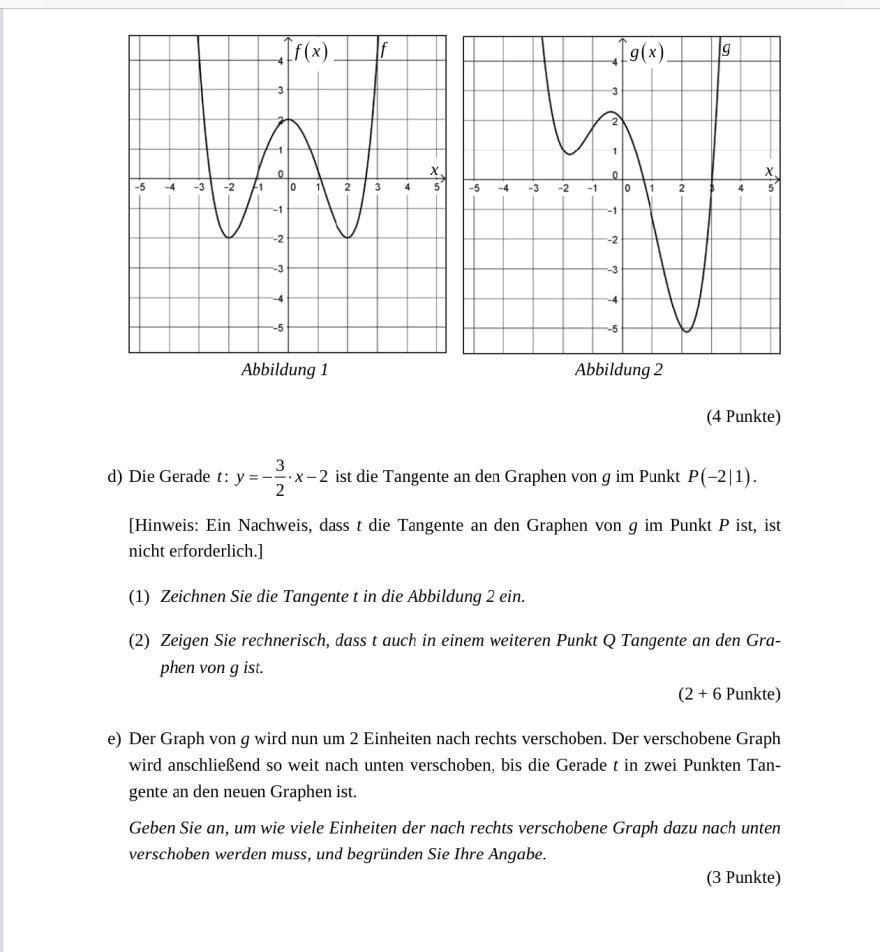
Abbildung 1
Abbildung 2
(4 Punkte)
d) Die Gerade \( t: y=-\frac{3}{2} \cdot x-2 \) ist die Tangente an den Graphen von \( g \) im Punkt \( P(-2 \mid 1) \).
[Hinweis: Ein Nachweis, dass \( t \) die Tangente an den Graphen von \( g \) im Punkt \( P \) ist, ist nicht erforderlich.]
(1) Zeichnen Sie die Tangente \( t \) in die Abbildung 2 ein.
(2) Zeigen Sie rechnerisch, dass \( t \) auch in einem weiteren Punkt \( Q \) Tangente an den Graphen von \( g \) ist.
(2 + 6 Punkte)
e) Der Graph von \( g \) wird nun um 2 Einheiten nach rechts verschoben. Der verschobene Graph wird anschließend so weit nach unten verschoben, bis die Gerade \( t \) in zwei Punkten Tangente an den neuen Graphen ist.
Geben Sie an, um wie viele Einheiten der nach rechts verschobene Graph dazu nach unten verschoben werden muss, und begründen Sie Ihre Angabe.
(3 Punkte)
Problem/Ansatz: Die Funktion von g lautet 1/4x4- 2x2-3/2x+2 , mit der Verschiebung um 2 Einheiten nach rechts gilt dann g(x-2). Aber ich finde nicht, dass eine Verschiebung nach unten nötig wäre, da man auch eine Tangente an den Lokalen Maximal/Minimalstellen berechnen kann. Ist das richtig ? Und wenn nicht, wie kann ich die weitere Verschiebung berechnen ?