Bestimmen Sie den Winkel 0 ≤ α ≤ 180° für den gilt:

Question

Hallo ich brauche dringend Hilfe bei folgende Aufgabe

Bestimmen Sie den Winkel 0 ≤ α ≤ 180° für den gilt:

a) sin(α − 72°) = sin(α)

b) cos(α + 16°) = cos(α)

Es wurde schon einmal die selbe Frage gestellt jedoch hat mir die Antwort nicht weitergeholfen. Es wäre wirklich nett wenn mir jemand Den ganzen rechen Weg sagen könnte und zusätzlich welche Additionstheoreme angewendet werden müssen.

Answer 1

a)
Theoreme:

sin(x+y) = sin(x)*cos(y) + cos(x)*sin(y)
sin(x-y) = sin(x)*cos(y) - cos(x)*sin(y)

sin(α -72°) = sin(α )

Subst. b = α - 36° → α = b+36°

sin((b+36°)-72°) = sin(b+36°)
sin(b-36°) = sin(b+36°)

Theoreme anwenden:

sin(b)*cos(36°) - cos(b)*sin(36°) = sin(b)*cos(36°) + cos(b)*sin(36°)
-cos(b)*sin(36°) = cos(b)*sin(36°)
-cos(b) = cos(b)

Das gilt für b=90° oder b=270°, daraus folgt α =126° oder α =306° (mit der Periode 180°)

b)
Theoreme:

cos(x+y) = cos(x)*cos(y) - sin(x)*sin(y)
cos(x-y) = cos(x)*cos(y) - sin(x)*sin(y)

cos(α +16°) = cos(α)

Subst. b = α + 8° --> α = b-8°

cos((b-8°)+16°) = cos(b-8°)
cos(b+8°) = cos(b-8°)

Theoreme anwenden:

cos(b)*cos(8°) - sin(b)*sin(8°) = cos(b)*cos(8°) + sin(b)*sin(8°)
- sin(b)*sin(8°) = sin(b)*sin(8°)
- sin(b) = sin(b)

Das gilt für b= 180°, daraus folgt α=172° (mit der Periode 360°)

Answer 2

Die Funktion \(f(x) = \sin(x)\) ist achsensymmetrisch bezüglich der Geraden \(x = 90°\).

Die Funktion \(g(x) = \sin(x-72°)\) ist gegenüber der Funktion \(f\) um \(72°\) nach rechts verschoben. Sie ist also achsensymmetrisch bezüglich der Geraden \(x = 90°+72°=162°\).

In der Mitte zwischen den beiden Geraden liegt die Gerade \(x = \frac{90° + 162°}{2}=126°\).

Comments

Aber dann habe ich doch kein Additionstheorem angewendet oder?

---

Es müssen keine Additionstheoreme angewendet werden.

---

Aber dann habe ich doch kein Additionstheorem angewendet oder?

Brauchst du doch auch nicht.

Wenn sich zwei Winkel mit dem gleichen Sinuswert um 72° unterscheiden, kann der eine 36° nach 90° und der andere 36° vor 90° liegen.

Bei b) liegt z.B. der eine Winkel 8° über 0° und der andere 8° unter 0°

ODER

der eine Winkel 8° über 180° und der andere 8° unter 180°.

Answer 3

a)

Du suchst 2 Winkel die symmetrisch um 90° liegen und voneinander um 72° entfernt sind. D.h. beide haben zu 90° eine Entfernung von 72°/2 = 36°.

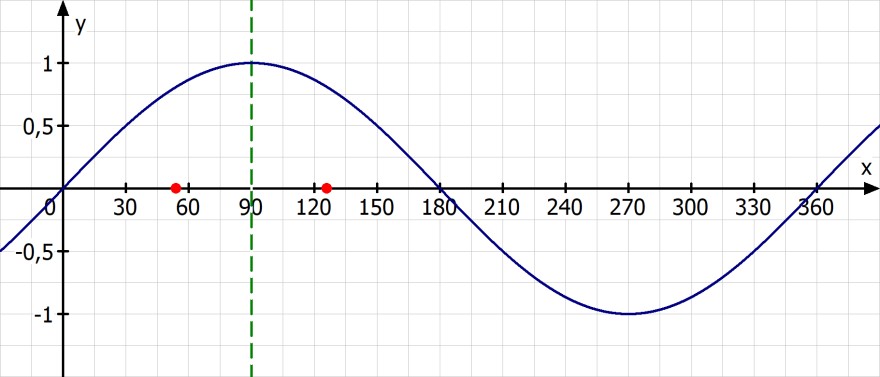
Es gilt also

α = 90° + 36° = 126°
α - 72° = 126° - 72° = 54°

Kannst du das so nachvollziehen.

b)

Du suchst zwei Winkel im Abstand von 16°. Die also zu einer Symmetrieachse einen Abstand von 8° besitzen.

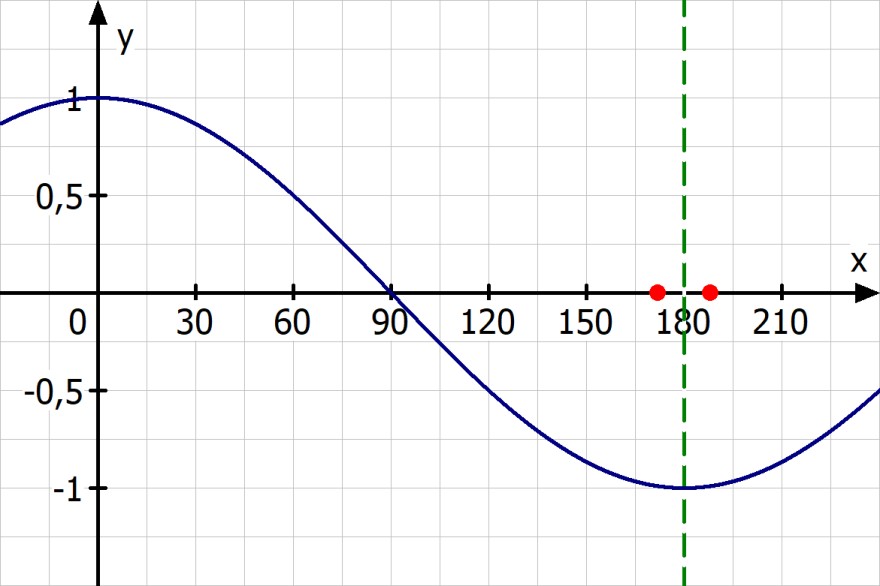
Es gilt hier

α = 180° - 8° = 172°

α + 16° = 180° + 8° = 188°

Comments

Sorry. Man sollte das nicht so zwischendurch ohne richtig zu lesen machen und zweitens sollte man sich eine Skizze machen.

Ich habe meine Lösung für b) oben ergänzt.