Untersuchen Sie die folgende Reihe auf Konvergenz und bestimmen Sie ggf. Den Grenzwert.

Question 1

Aufgabe:

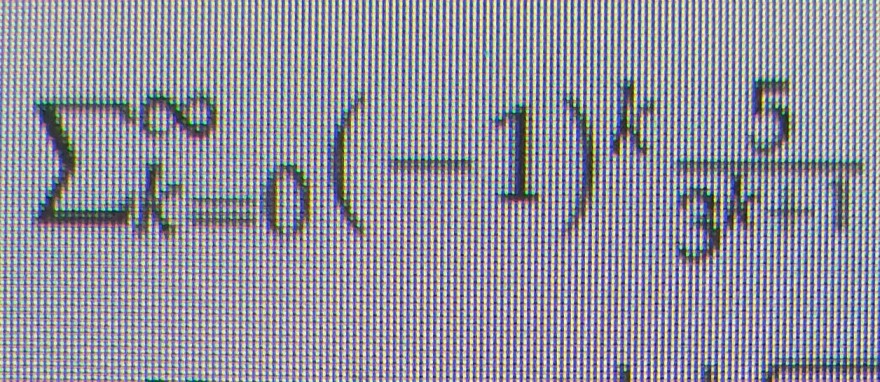
Text erkannt:

$ \sum \limits_{k=0}^{\infty}(-1)^{k} \frac{5}{3^{k+1}} $

Können Sie mir bitte, bei dieser Aufgabe helfen, damit ich das besser verstehe und mit dem Prinzip den Rest selber versuche?

Ich werde sehr dankbar.

Question 2

Aloha :)$$S=\sum\limits_{k=0}^\infty(-1)^k\,\frac{5}{3^{k+1}}=\sum\limits_{k=0}^\infty\frac{5\cdot(-1)^k}{3\cdot3^k}=\frac53\sum\limits_{k=0}^\infty\left(-\frac13\right)^k$$Die Summe entpuppt sich als eine geometrische Reihe, für die gilt:$$\sum\limits_{k=0}^\infty q^k=\frac{1}{1-q}\quad\text{für}\quad|q|<1$$Offensichtlich ist $q=-\frac13$ und damit die Bedingung für Konvergenz $(|q|<1)$ erfüllt:$$S=\frac53\cdot\frac{1}{1-\left(-\frac13\right)}=\frac53\cdot\frac{1}{\frac43}=\frac53\cdot\frac34=\frac54$$

Question 3

Ich bedanke mich bei dir :)

Tschakabumba · Answer 1 · 2022-05-31T16:35:18+0000

Aloha :)$$S=\sum\limits_{k=0}^\infty(-1)^k\,\frac{5}{3^{k+1}}=\sum\limits_{k=0}^\infty\frac{5\cdot(-1)^k}{3\cdot3^k}=\frac53\sum\limits_{k=0}^\infty\left(-\frac13\right)^k$$Die Summe entpuppt sich als eine geometrische Reihe, für die gilt:$$\sum\limits_{k=0}^\infty q^k=\frac{1}{1-q}\quad\text{für}\quad|q|<1$$Offensichtlich ist $q=-\frac13$ und damit die Bedingung für Konvergenz $(|q|<1)$ erfüllt:$$S=\frac53\cdot\frac{1}{1-\left(-\frac13\right)}=\frac53\cdot\frac{1}{\frac43}=\frac53\cdot\frac34=\frac54$$

Untersuchen Sie die folgende Reihe auf Konvergenz und bestimmen Sie ggf. Den Grenzwert.

1 Antwort

Ähnliche Fragen

Eingabetools:

Beliebte Fragen:

Heiße Lounge-Fragen: