Aufgabe:
Untersuchen Sie die folgenden Reihen auf Konvergenz und bestimmen Sie gegebenenfalls den Grenzwert.
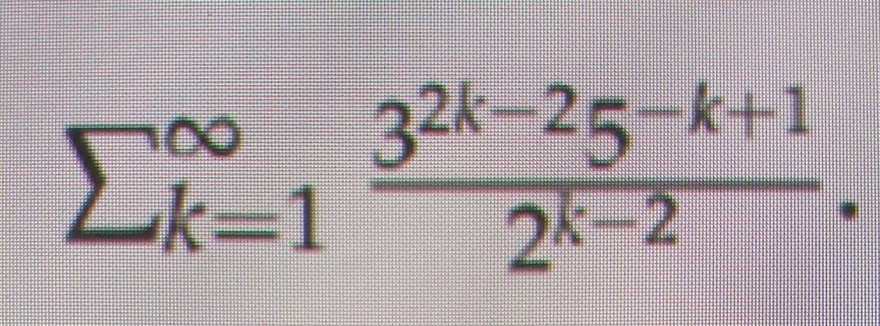
Text erkannt:
\( \sum \limits_{k=1}^{\infty} \frac{3^{2 k-2} 5^{-k+1}}{2^{k-2}} \)
Problem/Ansatz:
Das ist meine Lösung. Können Sie mir bitte sagen, ob das richtig oder falsch ist? Wenn das falsch ist, können Sie mir das bitte vorrechnen, weil ich nicht weiter komme.
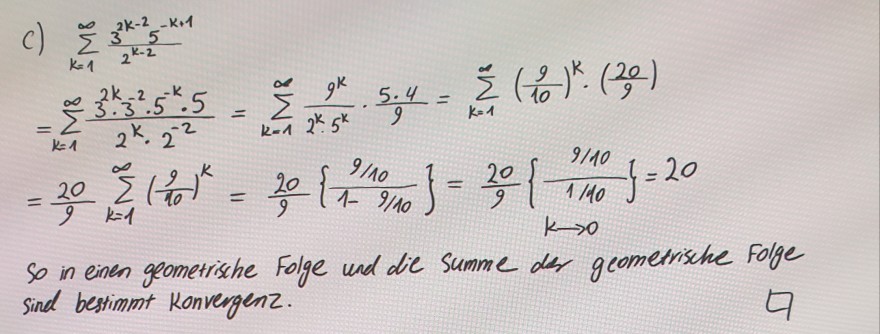
Text erkannt:
\( \text { C) } \begin{aligned} & \sum \limits_{k=1}^{\infty} \frac{3^{2 k-2} 5^{-k+1}}{2^{k-2}} \\ =& \sum \limits_{k=1}^{\infty} \frac{3^{2 k} \cdot 3^{-2} \cdot 5^{-k} \cdot 5}{2^{k} \cdot 2^{-2}}=\sum \limits_{k=1}^{\infty} \frac{9^{k}}{2^{k} \cdot 5^{k}} \cdot \frac{5 \cdot 4}{9}=\sum \limits_{k=1}^{\infty}\left(\frac{9}{10}\right)^{k} \cdot\left(\frac{20}{9}\right) \\ =& \frac{20}{9} \sum \limits_{k=1}^{\infty}\left(\frac{9}{10}\right)^{k}=\frac{20}{9}\left\{\frac{9 / 10}{1-9 / 10}\right\}=\frac{20}{9}\left\{\frac{9 / 10}{1 / 40}\right\}=20 \end{aligned} \)
So in einen geometrishe Folge und die summe der geometrische Folge sind bestimmt Konvergenz.