Wie groß ist die Summe der Quadrate der 9 Abstände?

Question

Gegeben ist ein regelmäßiges Zehneck, dessen Eckpunkte auf einem Kreis mit Radius 1 liegen. Jemand wählt einen Eckpunkt des Zehnecks aus und bestimmt die Abstände von diesem Punkt zu den 9 übrigen Eckpunkten des Zehnecks. Wie groß ist die Summe der Quadrate der 9 Abstände?
(Hinweis: Thales und Pythagoras)

Answer 1

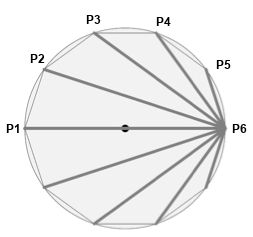
Es reicht einen speziellen Fall zu berechnen, denn die Wahl des Eckpunktes spielt für das Ergebnis keine Rolle.

Koordinaten P1: cos(180), sin(180) = (-1,0)
Koordinaten P2: cos(144), sin(144)
Koordinaten P3: cos(108), sin(108)
Koordinaten P4: cos(72), sin(72)
Koordinaten P5: cos(36), sin(36)
Koordinaten P6 (Ausgangspunkt) : cos(0,sin(0) = (1,0)

d^2(P6,P1) = 4
d^2(P6,P2) = (1 - cos(144))^2 + (0 - sin(144))^2 = 2(1-cos(144))
d^2(P6,P3) = (1 - cos(108))^2 + (0 - sin(108))^2 = 2(1-cos(108))
d^2(P6,P4) = (1 - cos(72))^2 + (0 - sin(72))^2 = 2(1-cos(72))
d^2(P6,P5) = (1 - cos(36))^2 + (0 - sin(36))^2 = 2(1-cos(36))

Die Summe der quadratischen Abstände P2-P5 beträgt 8.

Die Summe aller 9 quadratischen Abstände somit 4+8+8 = 20

Answer 2

Der Punkt P7 ist der an P1P6 gespiegelte Punkt P5.

Somit gilt nach Thales und Pythagoras (P6P2)²+(P6P5)²=(P6P2)²+(P6P5')²==(P6P2)²+(P6P7)²=(2r)²=4.

Gleiche Überlegungen für die hier nicht eingezeichneten Durchmesser P3P8, P4P9, P5P10.

Comments

P1P2^2 + P2P6^2 = P6P5^2 + P6P2^2 = P1P6^2 = 4
4*4  + 4 = 20