Hallo,
Die kanonischen Basisvektoren des \(\mathbb R^3\) sind$$e_1=\begin{pmatrix}1\\ 0\\ 0\end{pmatrix},\space e_2=\begin{pmatrix}0\\ 1\\ 0\end{pmatrix},\space e_3=\begin{pmatrix}0\\ 0\\ 1\end{pmatrix}$$Die Ebene \(E\), die durch die beiden oben angegeben Vektoren erzeugt wird, lässt sich in der Hesseschen Normalform schreiben:$$\begin{pmatrix}1\\ 0\\ 1\end{pmatrix} \times \begin{pmatrix}3\\ 1\\ -1\end{pmatrix} = \begin{pmatrix}-1\\ 4\\ 1\end{pmatrix} \\ \implies E: \quad \frac1{3\sqrt{2}} \begin{pmatrix}-1\\ 4\\ 1\end{pmatrix} \vec x = 0$$Um die orthogonale Projektion eines beliebigen Vektors zu berechnen, bestimmt man den Abstand des Vektor(Endes) von der Ebene und zieht den Normalenvektor von \(E\) multipliziert mit diesem Abstand davon ab. Warum das so ist, sollte aus der folgenden Skizze hervorgehen (um den Faktor 4 vergrößert):
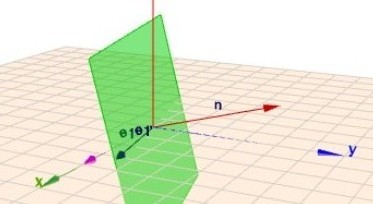
Der mangenta-farbende Vektor ist \(e_1\) und seine Projektion der schwarze Vektor in der grünen Ebene. Klick auf das Bild und schaue es Dir bitte an wie man zu dem schwarzen Vektor \(e_1'\) kommt. Hier wird der Differenzvektor (rot) addiert, da der 'Abstand' \(d_1\) negativ ist. Die Rechnung ist:$$d_1 = \frac1{3\sqrt{2}} \begin{pmatrix}-1\\ 4\\ 1\end{pmatrix} \cdot \begin{pmatrix}1\\ 0\\ 0\end{pmatrix} = - \frac1{3\sqrt{2}} \\\implies e_1' = \begin{pmatrix}1\\ 0\\ 0\end{pmatrix} + \frac1{18}\begin{pmatrix}-1\\ 4\\ 1\end{pmatrix} = \frac1{18} \begin{pmatrix}17\\ 4\\ 1\end{pmatrix} $$Dasselbe macht man nun für die beiden anderen Basisvektoren:$$e_2' =\frac1{18} \begin{pmatrix}4\\ 2\\ -4\end{pmatrix} ,\quad e_3'=\frac1{18}\begin{pmatrix}1\\ -4\\ 17\end{pmatrix}$$womit Aufgabenteil (a) erledigt wäre. Und für (b) braucht man die drei Spaltenvektoren nur noch zu einer Matrix \(M\) zusammen fassen:$$ M = \frac1{18}\begin{pmatrix}17& 4& 1\\ 4& 2& -4\\ 1& -4& 17\end{pmatrix}$$Allgemein gilt: Ist der Einheitsvektor \(n\) der Ursprungsebene gegeben, so ist die Matrix für die Projektion auf diese Ebene$$M = \underline{1} - nn^T \quad |n| = 1$$Beachte, dass es sich bei \(nn^T\) um das dyadische Produkt der Vektoren handelt.
Gruß Werner