Zeigen sie, dass h3 • V(Kegel groß) = H3 •V(Kegel klein) gilt.

Question

Aufgabe:

Vorgelegt sei ein Kegel mit Radius R und Höhe H. Diesem sei ein kleinerer Kegel mit Radius r und Höhe h wie in folgender Figur beschrieben. Grundflächen der Kegel sind parallel.

Zeigen sie, dass h³ • V(Kegel groß) = H³ •V(Kegel klein) gilt.

Answer 1

Volumen Kegel klein: Vk = 1/3 · π · r^2 · h

Volumen Kegel gross: Vg = 1/3 · π · R^2 · H

Behauptung:

1/3 · π · r^2 · h * H^3 = 1/3 · π · R^2 · H * h^3

r^2 · h * H^3 = R^2 · H * h^3

r^2 · H^2 = R^2 · h^2

\( \frac{r^2}{R^2} \) = \( \frac{h^2}{H^2} \)

\( \frac{r}{R} \) = \( \frac{h}{H} \)

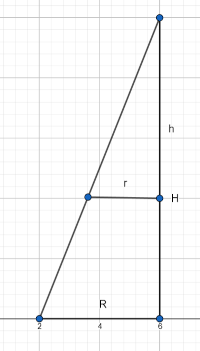
Dieses Verhältnis gilt aufgrund des Strahlensatzes für kongruente Dreiecke. Siehe dazu folgendes Bild (halber Querschnitt durch den Kegel):

 

Comments

Vielen Dank!

Könnten sie das mit dem Strahlensatz genauer erklären?

---

Habe meine Antwort um ein Bild ergänzt.