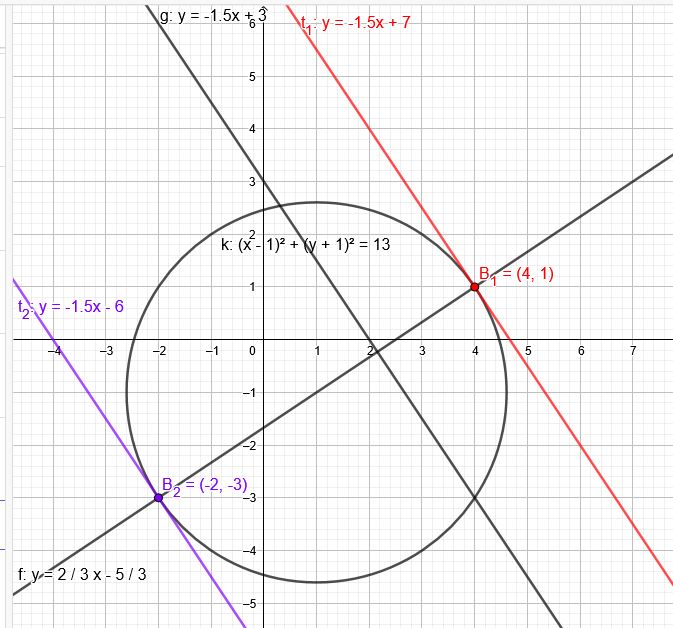
Ermittle Gleichungen der Tangenten an den Kreis k, die parallel zur Geraden g sind, und gib die Koordinaten der Berührpunkte an.
k:\((x-1)^2+(y+1)^2=13\); g: \(y= -1,5x+3\) mit \(m=-\red{1,5}\)
\(k(x,y)=(x-1)^2+(y+1)^2-13\)
\(k_x(x,y)=2(x-1)\)
\(k_y(x,y)=2(y+1)^2\)
\(k'(x)=-\frac{k_x(x,y)}{k_y(x,y)}=-\frac{x-1}{y+1}\)
\(-\red{1,5}=-\frac{x-1}{y+1}\)
Die Gerade \(y=\frac{2}{3}x-\frac{5}{3}\) schneidet den Kreis \(k\) in den beiden Berührpunkten.
Tangentenberechnung dann mit der Punkt-Steigungsform der Geraden.