Vom Duplikat:
Titel: Wie beschreibe ich das?
Stichworte: graph,funktion,parabel,nullstellen
Aufgabe:
Der Graph von t berührt an der Stelle x1=1 den Graphen von f.
An der Stelle x2=4 hingegen schneidet der Graph von t den Graphen von f (siehe Abbildung).
Beschreiben sie, wie man in dem hier vorliegenden Fall den Unterschied zwischen Berühren und Schneiden anhand von Funktionswerten von d erkennt.
Gegeben: f(x)=-1/3*x3+3*x2-8/3*x+2
t(x)=1/3*x+2/3
d(x)= -1/3*x3+2*x2-3*x+4/3
die Funktion d besitzt die Nullstellen X1=1 und x2=4
Problem/Ansatz:
Wie beschreibe ich das? 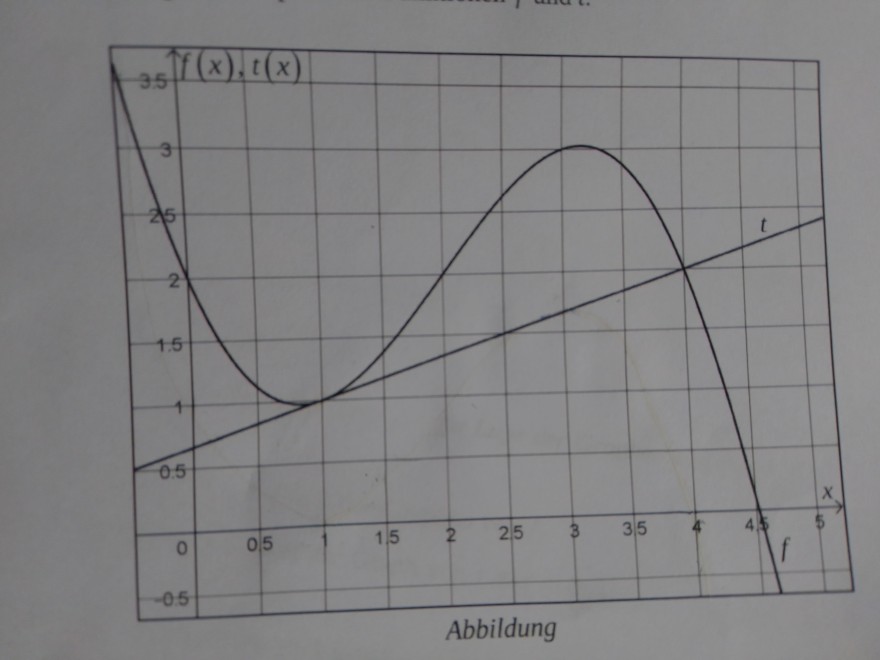
Text erkannt:
Abbildung