Bestimmen Sie die Dimension des Kerns und des Bildes eines 2x2 Matrix

Question

hello

kann jemand mir helfen wie man diese Aufgabe berechnen kann :)

ich habe viele youtube Videos angeschaut, aber alle waren für 3x3 oder 4x4 Matrix, deswegen ich weiß nicht wie man mit 2x2 Matrix umgeht.

Danke im Voraus ^^  

Text erkannt:

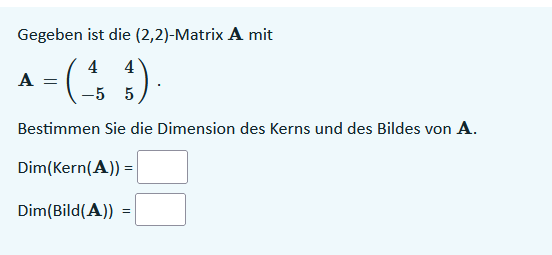
Gegeben ist die (2,2)-Matrix \( \mathbf{A} \) mit
\( \mathbf{A}=\left(\begin{array}{cc} 4 & 4 \\ -5 & 5 \end{array}\right) \text {. } \)
Bestimmen Sie die Dimension des Kerns und des Bildes von \( \mathbf{A} \).
\( \begin{array}{l} \operatorname{Dim}(\operatorname{Kern}(\mathbf{A}))=\square \\ \operatorname{Dim}(\operatorname{Bild}(\mathbf{A}))=\square \end{array} \)

Answer 1

Für die Berechnung von dim(Bild(A)) musst du einfach nur den Rang der Matrix berechnen, das ergibt dasselbe.

Dim(Ker(A)) kannst du bestimmen, indem du die Spaltenanzahl/Zeilenanzahl minus den Rang der Matrix berechnest.

Answer 2

Hallo

Du musst das ja lernen, so löse für Kern A*x =0 ein wirklich einfaches GS .  Dann hast du auch direkt dim Bild

für Bild bestimme z.B. Bild von (1,0) und (0,1)

anderer Weg: du weisst wie dim Bild  oder dim Kern von der Determinante abhängt?

Gruß lul