Aufgabe: Sensitivität: Wahrscheinlichkeit, dass bei einer kranken Person der Test positiv ausfällt
• Spezifität: Wahrscheinlichkeit, dass eine gesunde Person als gesund identifiziert wird
(a) Wir nehmen an, dass in einer Bevölkerungsgruppe ca. 6% aktuell das SARS-CoV-2- Virus in sich tragen. Ein Rapid-Antigen Test hat laut Herstellungsfirma eine Spezifität von 99,68 % und eine Sensitivität von 96,52 %.
Stellen Sie diesen Sachverhalt in einem Baumdiagramm dar und berechnen Sie:
(i) die Wahrscheinlichkeit, dass eine Person infiziert ist und ein positives Testergebnis erhält.
(ii) die Wahrscheinlichkeit für ein positives Testergebnis,
(iii) die Wahrscheinlichkeit, dass jemand mit einem negativen Testergebnis das Virus in
sich trägt.
Problem/Ansatz:
Die 1-3 hab ich noch nicht gemacht da ich mich erst vergewissern wollte ob mein Baumdiagramm so richtig ist: (C ist hier infizierte Person und P ein positiver Test)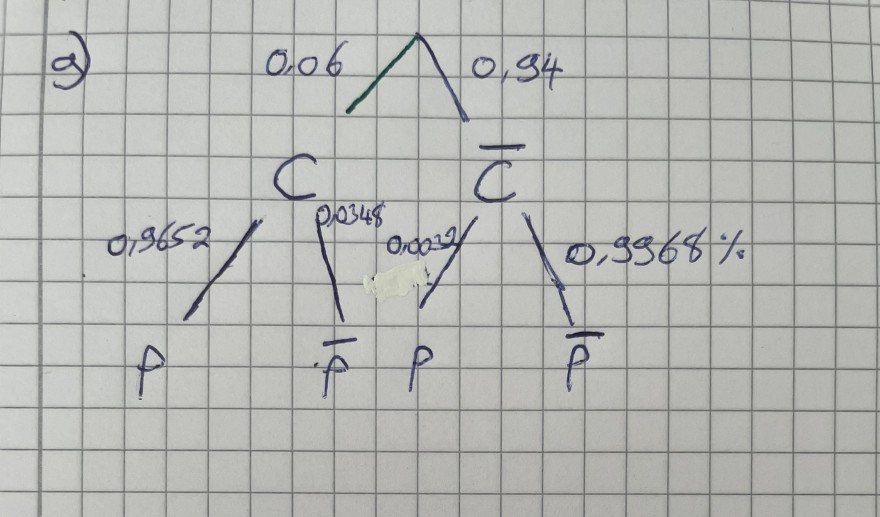
Text erkannt:
g) \( 0,06 / 0,94 \)