Aufgabe: Berechnen Sie im Falle der Konvergenz den Grenzwert oder begründen Sie, weshalb der jeweilige Grenzwert nicht existiert. Die Aufgaben sollen ohne der Anwendung der Regel von l'Hospital gelöst werden.
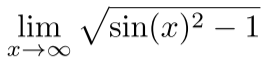
Ansatz für diese Aufgabe: Der Grenzwert existiert nicht, da die Sinusfunktion für ∞ nicht definiert ist. Frage: Lässt sich hier die Sinusfunktion irgendwie entfernen bzw. auflösen durch irgendeinen Trick oder existiert er hier wirklich nicht?

Ansatz: Ich habe versucht mittels Eins-Ergänzung das x aus dem Nenner zu bekommen, damit ich die 4 einfach einsetzen kann aber egal wie ich es drehe und wende, ich erhalte immer eine Nullsumme im Nenner... Vielleicht sieht jemand den Trick, den man hier braucht oder kann mir anderweitig weiterhelfen?