Maximale Wasseroberfläche in einem rotierenden Würfel

Question

Aufgabe:

Ein Würfel mit der Kantenlänge 10cm wird zur Hälfte mit Wasser befüllt. Um welche Winkel muss der Würfel gekippt werden, damit die Wasseroberfläche maximal wird?

Problem/Ansatz:

In den meisten Fällen nimmt die Wasseroberfläche die Form eines Vierecks an. (Steht der Würfel senkrecht auf einer Ecke, entsteht ein regelmäßiges Sechseck ; diese Form wollte ich erstmal für meinen Ansatz vernachlässigen )

Meine Idee ist die Längen der Wasseroberfläche durch Vektoren zu beschreiben, um über den Betrag des Vektorproduktes anschließend durch Differerenzien die Extrema des Flächeninhaltes zu berechnen. Mein Problem dabei ist, diese Vektoren in Abhängigkeit der beiden Drehwinkel auszudrücken.

Ich würde mich freuen, wenn jemand einen Tipp für mich hat, oder ne Idee ob es einen besseren Ansatz für die Aufgabe gibt. :)

LG

Answer 1

Ajee,

ich bezweifle mal, dass sich eine allgemeingültige Funktion aufstellen lässt ohne Fallunterscheidungen zu treffen?

Betrachte ein Kippen 0..45° über die x-Achse, wo sich das Volumen auf 2 Prismen verteilt.

T := Ein Eckpunkt T (0,-a,0) wird über die x-Achse abgesenkt im Winkel α

\(T:=\left(0, -a \; \operatorname{cos} \left( \alpha \right), -a \; \operatorname{sin} \left( \alpha \right) \right)\)

===>

w Vektor auf Kante zur y-Achse

\(w:=a \; \operatorname{tan} \left( \alpha_x \right) \; \left(0, -\operatorname{sin} \left( \alpha_x \right), \operatorname{cos} \left( \alpha_x \right) \right)\)

\(T_{\alpha x} \, :=  \, \left(0, \frac{-a}{\operatorname{cos} \left( \alpha_x \right)}, 0 \right)\)

und weiter zur Wasseroberfläche

\(T_v:= T_{\alpha x} + \frac{w}{\left|w\right|} \cdot \frac{a \; \operatorname{cos} \left( \alpha_x \right) - a \; \operatorname{sin} \left( \alpha_x \right)}{2 \; \operatorname{cos} \left( \alpha_x \right)}\)

Dann haben wir ein Model des Wasserstandes:

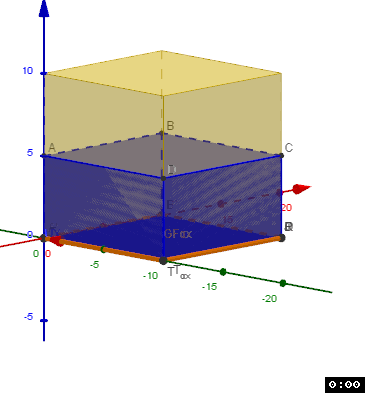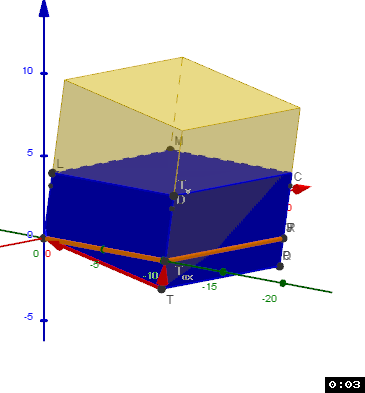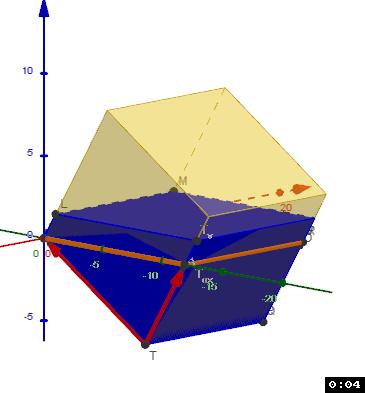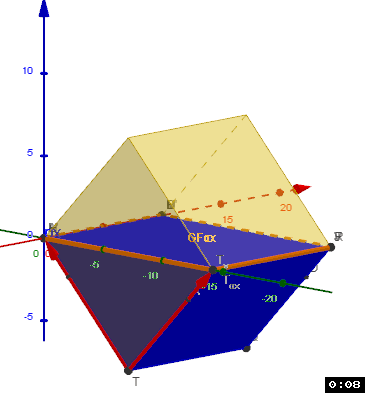
Du kannst ja mal was zu den Flächen herausziehen und vorstellen was dabei rum kommt?