Zeige, dass in (0,0) alle Richtungsableitungen von f existieren, f dort aber nicht total differenzierbar ist.

Question

Gegeben sei f: ℝ²→ℝ,

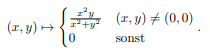
Text erkannt:

\( (x, y) \mapsto\left\{\begin{array}{ll}\frac{x^{2} y}{x^{2}+y^{2}} & (x, y) \neq(0,0) \\ 0 & \text { sonst }\end{array}\right. \)

Zeige, dass in (0,0) alle Richtungsableitungen von f existieren, f dort aber nicht total differenzierbar ist.