Zeige die Mengengleichheit: P(\bar{A} \cap \bar{B} \cap C \mid \bar{A} \cap \bar{B})=\frac{1}{2} wenn …

Question

Aufgabe:

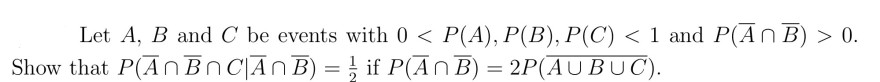
Text erkannt:

Seien \( A, B \) und \( C \) Ereignisse mit \( 0<P(A), P(B), P(C)<1 \) und \( P(\bar{A} \cap \bar{B})>0 \). Zeige, dass\( P(\bar{A} \cap \bar{B} \cap C \mid \bar{A} \cap \bar{B})=\frac{1}{2} \) wenn \( P(\bar{A} \cap \bar{B})=2 P(\overline{A \cup B \cup C}) \).

Problem/Ansatz:

kann uns bitte jemand bei der Lösung dieser Aufgabe helfen?

Wir sitzen bereits seit Stunden dran und kommen einfach nicht auf die Lösung.

Wir wären euch sehr dankbar!

Liebe Grüße

Answer 1

Hallo,

beachte, dass $$ \mathbb P(\bar A\cap\bar B\cap C|\bar A\cap\bar B)=\mathbb P(C|\bar A\cap\bar B)=1-\mathbb P(\bar C|\bar A\cap \bar B)$$

Die gegebene Bedingung \(\mathbb P(\bar A\cap\bar B)=2\mathbb P(\overline{A\cup B\cup C})\) liefert euch \( P(\bar C|\bar A\cap \bar B)=\frac{1}{2}\) indem ihr die rechte Seite umschreibt und dann benutzt, dass \(\mathbb P(E\cap F)=\mathbb P(E|F)\mathbb P(F)\) (für \(\mathbb P(F)>0\)) um \(\mathbb P(\bar C|\bar A\cap \bar B)\) zu erzeugen.

LG Dojima