Hallo,
du kannst die Punkte auch rechnerisch bestimmen:
\( \overrightarrow{O A}+\overrightarrow{B C}=\overrightarrow{O D} \)
\( \left(\begin{array}{l}5 \\ 7\end{array}\right)+\left(\begin{array}{c}-1 \\ -9\end{array}\right)=\left(\begin{array}{c}4 \\ -2\end{array}\right) \)
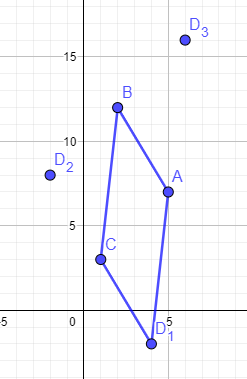
\( \overrightarrow{O C}+\overrightarrow{A B}=\overrightarrow{O D} \)
\( \left(\begin{array}{l}1 \\ 3\end{array}\right)+\left(\begin{array}{r}-3 \\ 5\end{array}\right)=\left(\begin{array}{r}-2 \\ 8\end{array}\right) \)

\( \overrightarrow{O B}+\overrightarrow{C A}=\overrightarrow{O D} \)
\( \left(\begin{array}{c}2 \\ 12\end{array}\right)+\left(\begin{array}{l}4 \\ 4\end{array}\right)=\left(\begin{array}{c}6 \\ 16\end{array}\right) \)
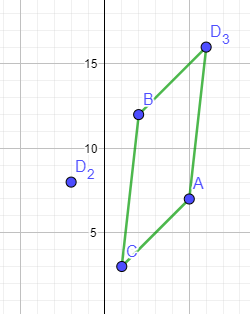
Gruß, Silvia