Aufgabe:
Man soll durch Umformen zeigen, dass die Wahrscheinlichkeit größer Null ist.
Problem/Ansatz:
folgendes ist gegeben: P(A∩B Ι C) und soll zeigen dass für folgende Wahrscheinlichkeit gilt: P(B | C ) > 0 .
Ich verstehe nicht ganz den Ansatz um die Aufgabe zu lösen.
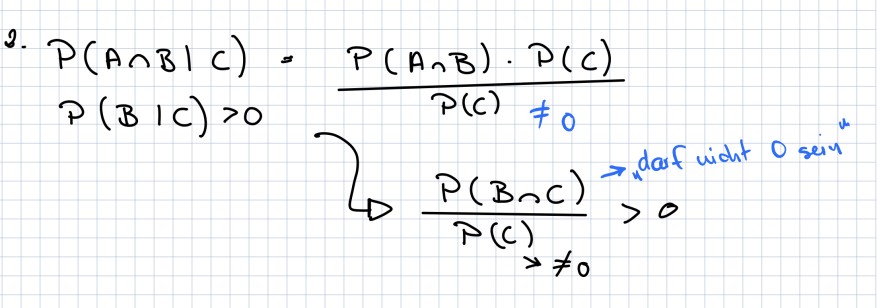
Text erkannt:
2. \( P(A \cap B \mid C)=\frac{P(A \cap B) \cdot P(C)}{P(C) \neq 0} \)