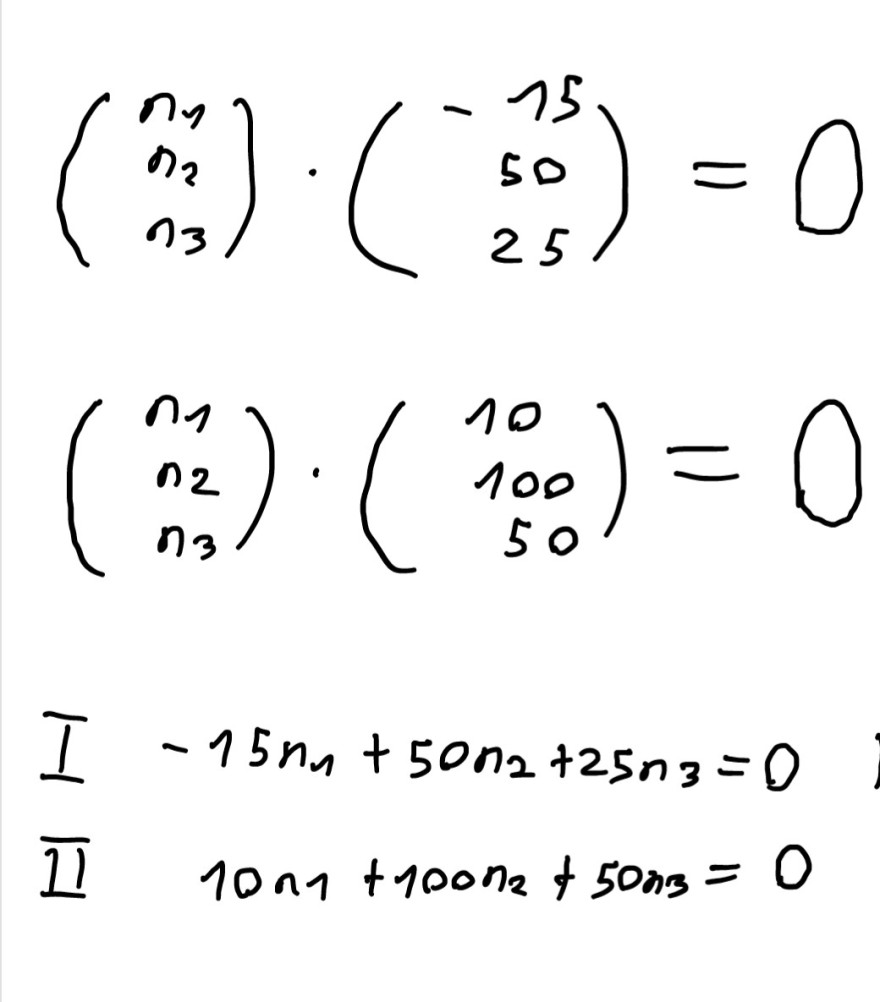2x3 Gleichungssystem lösen

Question

Aufgabe:

2x3 Gleichungssystem lösen

(2 Gleichungen, 3 Unbekannte)

Problem/Ansatz:

Beim Berechnen des Normalenvektors einer Ebene anhand ihrer zwei Richtungsvektoren kam ich auf das Problem, dass ich nicht weiter weiß wie ich dieses LGS lösen kann (im Anhang).

Würde mich über eine kurze Erläuterung dazu freuen mit der entsprechenden Rechnung, aus meiner Recherche im Internet und auf YouTube bin ich bisher nicht wirklich schlau geworden

Answer 1

Hallo,

wenn die Länge des Vektors nicht vorgegeben ist, darfst du eine Koordinate vorgeben. Aber erst einmal rechnen!

Ich nenne die drei Koordinaten x, y, z, damit ich leichter tippen kann.

-15x+50y+25z=0     |:5

-3x +10y +5z=0       (I)

10x+100y+50z =0      |:10

x+10y+5z=0            (II)

(II)-(I) -->x=0

10y+5z=0

--> z=-2y

Sei y=1 → z=-2

n=[0;1;-2]

:-)

Answer 2

Den Normalenvektor aus 2 Richtungsvektoren r1,r2 einer Ebene findet man über das Vektorprodukt

r1⊗r2 = (0, 1000, -2000)

und ADD

I+II ===>

\(  \left\{ n1 = 0, n2 = \frac{-1}{2} \; n3 \right\}  \)

n3 beliebig