Extremwert Aufgabe, Kugel

Question

Aufgabe

- Zielfunktion in Abhängigkeit von der Höhe des kegels
In eine Kugel mit dem Radius r = 1,5 cm soll ein Kegel mit maximalem Volumen einbeschrieben werden

- Hauptfunktion

- Zielfunktion

- erste Ableitung der Zielfunktion

-die null Stellen der App ersten Ableitung an

- zweite Ableitung Zielfunktion

-maximal Volumen des Kegels

-Höhe und Radius des Kegels

Comments

die null Stellen der App ersten Ableitung an

Was möchtest Du damit mitteilen?

Wie lautet die Aufgabe?

Answer 1

x^2 + y^2 = r^2 --> x = √(r^2 - y^2)

Zielfunktion

V = 1/3 * pi * √(r^2 - y^2)^2 * (r + y) = pi/3·(r^3 + r^2·y - y^3 - r·y^2)

V' = pi/3·(- 3·y^2 - 2·r·y + r^2) = 0 --> y = 1/3·r

Comments

Wichtig ist sich zuerst eine Skizze zu machen. Die nötigen Teile zu beschriften und wichtige Nebenbedingungen dabei aufzustellen. Dann kann man mit der Hauptfunktion auch die Zielfunktion aufstellen.

Answer 2

- Zielfunktion in Abhängigkeit von der Höhe des Kegels
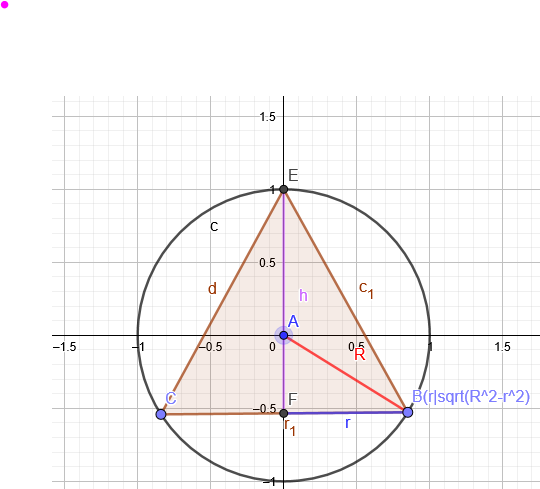
In eine Kugel mit dem Radius R = 1,5 cm soll ein Kegel mit maximalem Volumen einbeschrieben werden

\(V= \frac{1}{3}*π*r^2*h \) soll maximal werden.

 \((AF)^2=R^2-r^2\)

\(AF=\sqrt{R^2-r^2}\)

\(h=R+\sqrt{R^2-r^2}\)

\(h=1,5+\sqrt{2,25-r^2}\) Auflösen nach \(r^2\):

\(r^2=3h-h^2\)

\(V(h)= \frac{1}{3}*π*(3h-h^2)*h=\frac{1}{3}*π*(3h^2-h^3)\)

\(V´(h)=\frac{1}{3}*π*(6h-3h^2))\)

\(\frac{1}{3}*π*(6h-3h^2)=0\)

\(2h-h^2=0\)

1.)\(h=0\) kommt nicht in Betracht (Minimum)

2.)\(h=2\)

\(r^2=3*2-4\)

\(r=\sqrt{2} \)

Maximales Volumen:

\(V= \frac{1}{3}*π*2*2=\frac{4}{3}*π \)