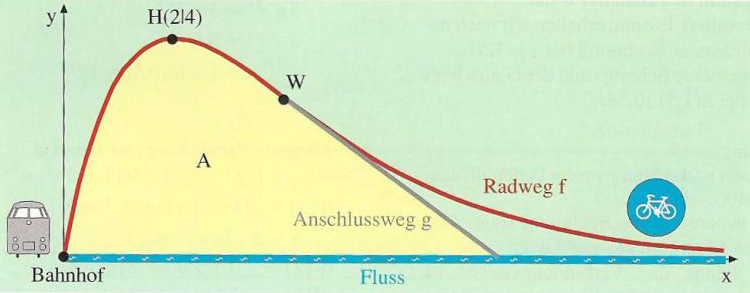
Der rot eingezeichnete Fahrradweg \( \mathrm{f} \) kann durch die Funktion \( \mathrm{f}(\mathrm{x})=2 \mathrm{x} \cdot \mathrm{e}^{\mathrm{ax}+\mathrm{b}} \) beschrieben werden. Sein nördlichster Punkt ist \( \mathrm{H}(2 | 4) . \) Von Westen nach Osten, d. h. auf der x-Achse, verläuft ein Fluss. 1 Längeneinheit entspricht 100 Metern. \( y^{4} \)
a) Bestimmen Sie die Parameter a und b, und skizzieren Sie den Graphen von f für \( 0 \leq x \leq 10 \).
b) Bestimmen Sie die Ableitungen \( \mathrm{f}^{\prime} \) und \( \mathrm{f}^{\prime \prime} \). In welchem Punkt W geht der Fahrradweg von einer Rechts- in eine Linkskurve über?
c) In welchem Winkel schneidet der Fahrradweg f den Fluss?