A bisschen viel verlangt bei dem umfangreichen auftrag, so ganz ohne eigenbeitrag,
affine normal form quadratisch ergänzen mit
\(T' \, := \, \left\{ x_o = x + y - \frac{5}{2} \; \sqrt{2}, y_o = y \right\} \)
==>
\(q_N: \, \sqrt{2} \; x_o^{2} + 4 \; y_o - \frac{25}{2} \; \sqrt{2} = 0\)
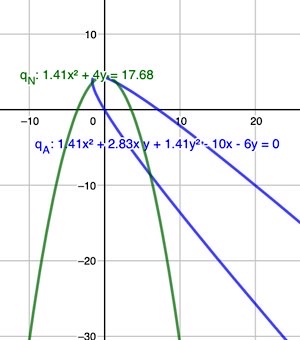
euklidische normalform
https://www.geogebra.org/m/jybmgrce