Pythagoras- Pyramide

Question

Gegeben ist eine quadratische Pyramide mir der Grundkantelänge a und der seitenlänge s.

(1) Zeige, dass für die Körperhöhe h gilt:
h= wurzel s^2 - 1/2 a^2

(2) Gib die Höhe hs einer Seitenfläche in Abhängigkeit von a und s an .


ich verstehe das net :/
danke im Voraus

Answer 1

also (1) kann ich nicht zeigen.

Nimm Dir mal eine Pyramide:

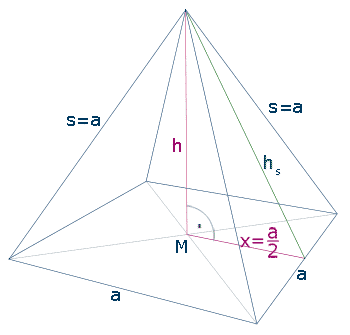
(Ignoriere mal das s=a) Du erkennst, dass ein rechtwinkliges Dreieck gebildet wird durch die halbe Diagonlae, s und h. Damit kannst Du also folgendes aufstellen:

s^2 = h^2-(d/2)^2

wobei d die Diagonale ist.

d^2 = 2a^2

d = √2*a

Damit in die ursprüngliche Gleichung:

h^2 = s^2+(√2*a/2)^2 = s^2+1/2*a^2

h = √(s^2+1/2*a^2)

b)

Nun gilt für h_s siehe Skizze:

h_s = √(s^2-(a/2)^2)

(Man hätte es auch über h ausdrücken können und dann in a) hergeleitete Beziehung einsetzen können..)

Alles klar?

Grüße