Hallo zusammen,
ich habe folgendes Problem:
Ich bin gerade dabei die Kovarianz zweier Zufallsvariablen U=2x+3y und V=3x−y auszurechnen. Zur Berechnung der Kovarianz brauche ich die Erwartungswerte E(U),E(V), E(UV). Dafür habe ich soweit alles aufgestellt (siehe Bild).
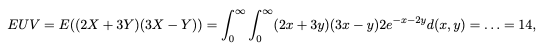
Text erkannt:
\( E U V=E((2 X+3 Y)(3 X-Y))=\int \limits_{0}^{\infty} \int \limits_{0}^{\infty}(2 x+3 y)(3 x-y) 2 e^{-x-2 y} d(x, y)=\ldots=14 \)
Jedoch ist mir unklar, wie genau ich das ausrechne, so dass zum Schluss "14" rauskommt.
Kann mir vielleicht jemand erklären, wie der Rechenweg zur Berechnung des Erwartungswerts E(UV) ist?
Vorab herzlich Dank!