Monotonieverhalten von f auf dem Intervall I [0;3]. Ableitungsfunktion f'(x) = (x-2)*(x^2+1)

Question

gegeben ist die ableitungsfunktion f'(x) = (x-2)*(x^2+1)

ich hab die nullstellen der ableitung berechnet, diese sind 2,1 und -1

wie geht es weiter? :/

Answer 1

 f'(x) = (x-2)*(x²+1)

Diese Ableitung hat nur die Nullstelle x=2

x^2 + 1 ≥ 1 > 0 (immer)

Für x>2 sind beide Faktoren grösser als 0. Die Funktion ist monoton steigend

Für x<2 ist der erste Faktor kleiner als 0 und der zweite grösser als 0. Die Funktion ist monoton fallend.

Answer 2

Hi,

da hast Du Dich vertan.

x^2+1 = 0

x^2 = -1

-> keine reelle Nullstellen.


Es gibt also nur x = 2 als Nullstelle.

Nun musst Du Dir überlegen, wann f'(x)>0 oder f(x)<0 ist.

Mach eine Punktprobe mit x = 0

f'(0) = -2*1 = -2

Folglich haben wir

fallend: x∈(-∞;2)

steigend: x∈(2;∞)


Klar?

Grüße

Answer 3

 

gegeben ist die ableitungsfunktion f'(x) = (x-2)*(x²+1)

ich hab die nullstellen der ableitung berechnet, diese sind 2,1 und -1

 

Das stimmt nicht ganz: Die einzige Nullstelle der Ableitung ist x₀ = 2, denn

f'(1) = (1-2) * (1²+1) = -1 * 2 = - 2 ≠ 0

f'(-1) = (-1-2) * ((-1)²+1) = -3 * 2 = - 6 ≠ 0

 

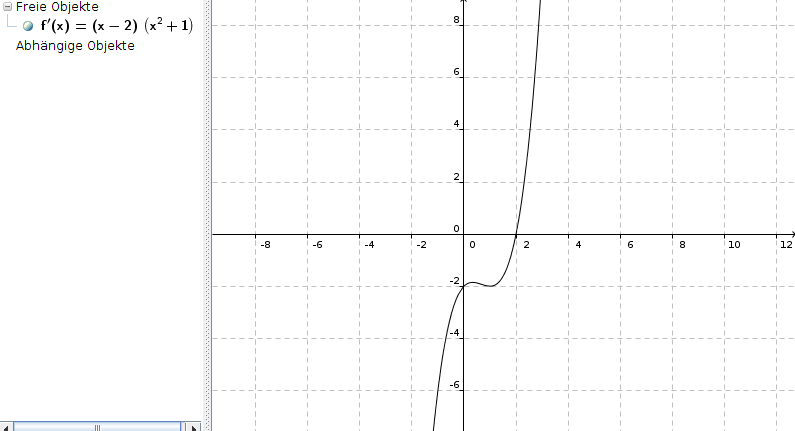
Ich würde jetzt die 2. Ableitung bilden, um sicherzustellen, dass an der Stelle x₀ = 2 wirklich ein Minimum liegt.

Dann setzt Du in die 1. Ableitung einen Wert < 2 ein, zum Beispiel 1:

f'(1) = -2 < 0, monoton fallend

und in die 1. Ableitung einen Wert > 2, zum Beispiel 3:

f'(3) = 1 * 10 > 0, monoton steigend

 

Besten Gruß