Aufgabe:
Bestimmen Sie die folgende Grenzwerte:
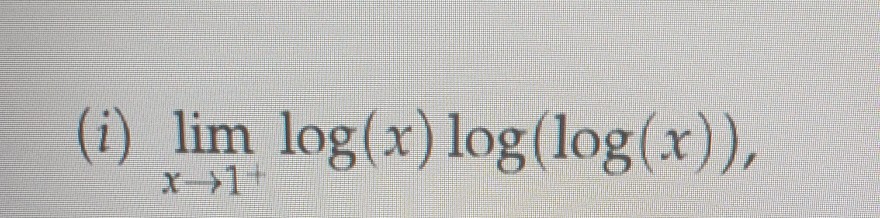
Text erkannt:
(i) \( \lim \limits_{x \rightarrow 1^{+}} \log (x) \log (\log (x)) \),
Problem/Ansatz:
Ich habe schon die Lösund aber ich verstehe eine Sache nicht!
Woher kommt die Ableitung 1/ log x in Musterlösung?
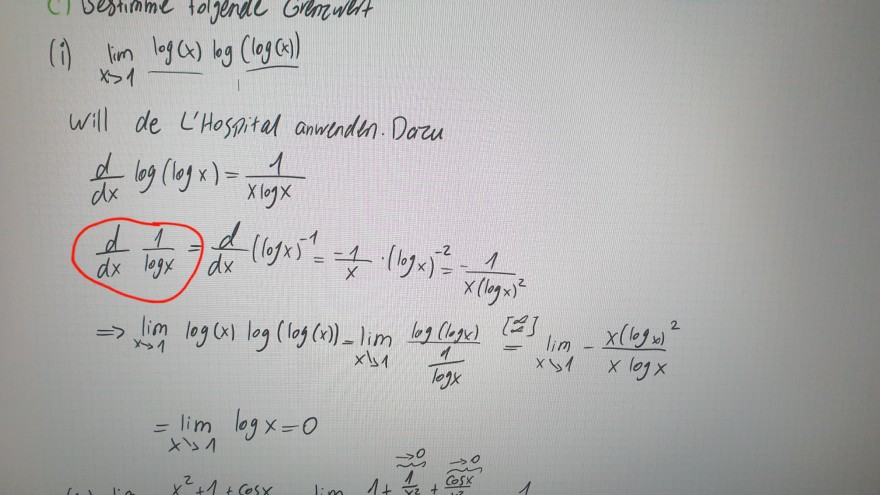
Text erkannt:
(i) \( \lim \limits_{x \rightarrow 1} \log (x) \log (\log (x)) \)
Will de L'Hosnital anwenden. Dozu
\( \begin{array}{l} \frac{d}{d x} \log (\log x)=\frac{1}{x \log x} \\ \frac{d}{d x} \frac{1}{\log x}=\frac{d}{d x}(\log x)^{-1}=\frac{-1}{x} \cdot\left(\log _{x}\right)^{-2}=-\frac{1}{x(\log x)^{2}} \\ \Rightarrow \lim \limits_{x \rightarrow 1} \log (x) \log (\log (x))=\lim \limits_{x \operatorname{lo}} \frac{\log (\log x)}{\frac{1}{\log x}}=\lim \limits_{x \rightarrow 1}-\frac{x(\log x)^{2}}{x \log x} \\ =\lim \limits_{x \rightarrow 1} \log x=0 \end{array} \)