Extremwertaufgabe mit "zeigen"

Question

Aufgabe:

Text erkannt:

7
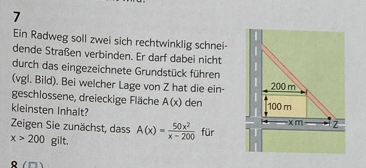
Ein Radweg soll zwei sich rechtwinklig schneidende Straßen verbinden. Er darf dabei nicht durch das eingezeichnete Grundstück führen (vgl. Bild). Bei welcher Lage von Z hat die eingeschlossene, dreieckige Fläche \( \mathrm{A}(\mathrm{x}) \) den kleinsten Inhalt?
Zeigen Sie zunächst, dass \( A(x)=\frac{50 x^{2}}{x-200} \) für \( x>200 \) gilt.

Problem/Ansatz:

Hallo ihr Lieben,

ich bräuchte mal Hilfe bei dieser Aufgabe. Nicht bei der Optimierung, aber bei dem Teil, "zeigen sie zunächst, dass ..... gilt."

Wir sollen den Strahlensatz verwenden. Aber ich habe keine Idee, wie ich mit diesem zeigen kann, dass A(x) rauskommt.

Vielen Dank im Voraus!

Answer 1

\( \frac{x-200}{100}=\frac{x}{y} \)

\( \frac{100}{x-200}=\frac{y}{x} \)

\( y=\frac{100x}{x-200}\)

Dreieckfläche:

\(A(x)=\frac{1}{2}*\frac{100x^2}{(x-200)}=\frac{50x^2}{x-200}\)

Comments

perfekt, ich danke dir! also musste ich den scheitelpunkt einfach auf z verlegen und y und 100 sind die parallelen. oh man bin ich blind. 1000 dank!

Answer 2

Hallo

Abschnitt senkrecht y

dann ist A=x*y/2 jetzt such einen Zusammenhang von x und y, dabei solltest du den Strahlensatz mit Spitze links oben und den 2 Parallelen  eine 200m die andere x lang  , wenn du das hast nach y auflösen und in A einsetzen

Mit den Tips mach dich mal selbst dran.

Gruß lul

Comments

Vielen dank lul,

also soweit war ich an sich schon. Fläche für rechtwinkliges Dreieck und Strahlensatz mit Scheitelpunkt oben an der Strecke y. x und 200 sind die Parallelen. Würde dann sagen x/200=y/y-100

aber das ist falsch :(