Über einen Fluss soll eine Brücke gebaut werden...

Question

Aufgabe:

Über einen Fluss soll eine Brücke gebaut werden. Der Querschnitt der zugehŏrigen Landschaft wird durch das Schaubild der Funktion \( f \) mit \( f(x)=-\frac{1}{2} x^{3}-\frac{3}{5} x^{2}+\frac{12}{5} \)

Der durchschnittliche Stand des Wassers wird in diesem Modell durch die \( x \) -Achse dargestellt.

1 LE entspricht \( 10 \mathrm{~m} \).

a) Bestimme die Breite und die Tiefe des Flusses

b) Schiffe, die \( 13 \mathrm{~m} \) aus dem Wasser ragen, sollen dazu in der Lage sein, unter der Brūcke durchzufahren.
Bestimme die minimale Länge der Brücke.

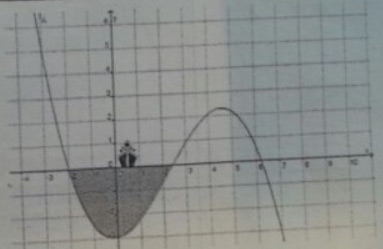
Ich habe zuerst gedacht, dass die funktion, die da oben steht  dem schaubild entspricht das tut es aber nicht.

Also habe ich durch die punkte f(-2)=0,f(0)=-3, f(-3),f(7)=-3

die Funktion mit f(x)= -1/10x³+2/3x²+7/30x-3 herausgefunden. Weiss aber nicht weiter.

Answer 1

f(x) = - 1/10·x³ + 2/3·x² + 7/30·x - 3

Nullstellen f(x) = 0

- 1/10·x³ + 2/3·x² + 7/30·x - 3 = 0

x = -2 oder x = 13/3 ± √34/3

Die Flussbreite ist der Abstand der beiden rechten Nullstellen also

2·√34/3 = 3.887301263 LE = 38.87 m


Extrempunkt f'(x) = 0

- 3·x²/10 + 4·x/3 + 7/30 = 0

x = -0.1686038657 ∨ x = 4.613048310

f(-0.1686038657) = -3.019910098 LE = -30.20 m


Länge der Brücke f(x) = 1.3

- 1/10·x³ + 2/3·x² + 7/30·x - 3 = 1.3

x = -2.320971810 ∨ x = 3.202428850 ∨ x = 5.785209626

3.202428850 - (-2.320971810) = 5.523400659 LE = 55.23 m

Comments

Die nullstelle müsste 2,38 sein. somit 48,38 m breit.

Die a hatte ich alleine hinbekommen nur die b hab ich immer noch nicht ganz verstanden was man da machen soll.

Also den ansatz hatte ich auch gemacht mit f von x glecih 1,3

Aber ich hatte die funktion danch so gelassen. wieso schauen sie hier nach den nullstellen.